 ◎ Transformer
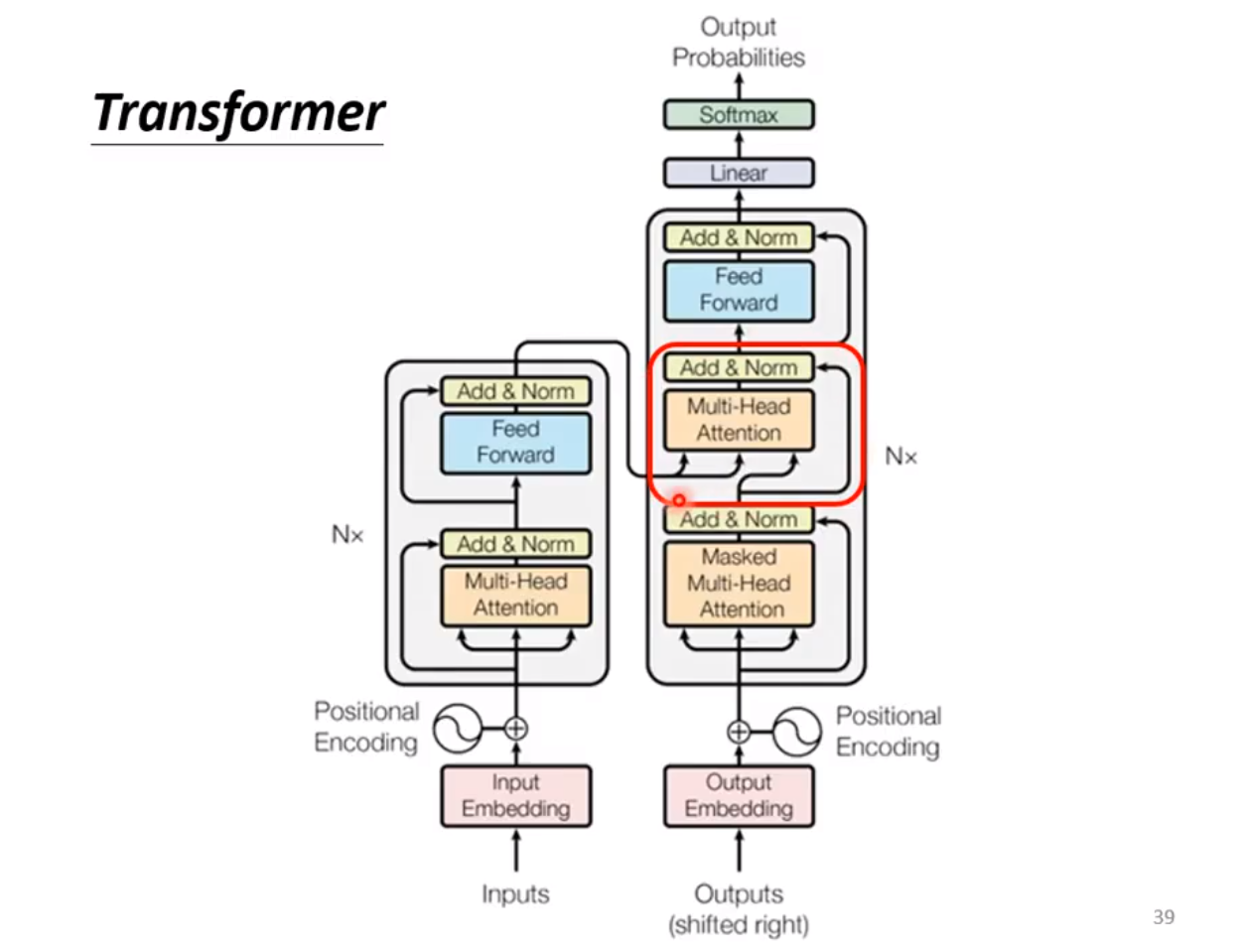
◎ Transformer
Attention 机制不是谷歌首先提出来的,但在在谷歌17年的论文《Attention is All You Need》中被很好地总结。这里贴出一篇很优秀的论文解读《Attention is All You Need》浅读(简介+代码),感兴趣的可以进一步去了解。
 ◎ 处理流程
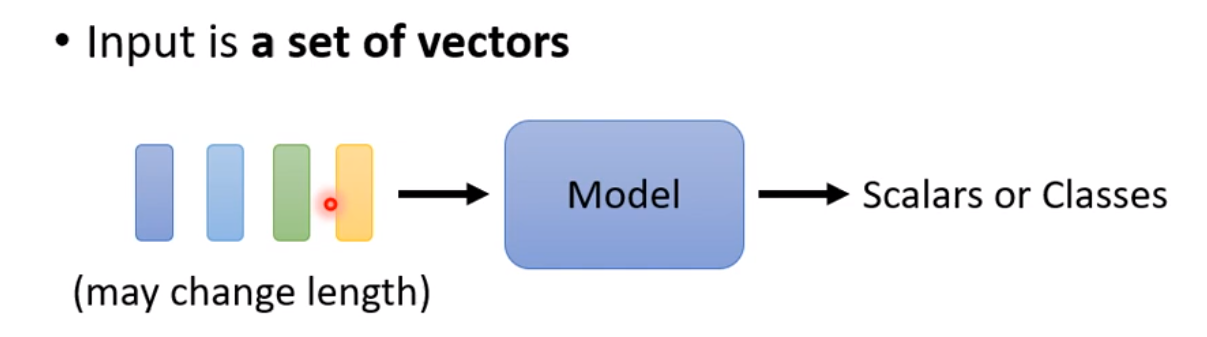
◎ 处理流程
在NLP的任务中,如词性识别,语音识别,文字翻译等,可以将文字通过文字嵌入(word embedding)的方式转化为向量的集合,或者将语音序列通过窗口裁切的方式转化为向量的集合, 然后通过RNN 或者 CNN 的方式完成序列的编码。RNN是一个马尔科夫决策过程,当前输入会依赖上一次的输出,CNN用局部窗口能捕捉到一定范围的结构信息。这两者要获得全局的信息必须得逐步进行(如RNN逐步递归,CNN通过多层卷积扩大感受野), 而Attention是一种一次计算可以得到全局信息的方法。
Self-attention 是 Attention中被用的最多的一种类型,下面简要介绍下Self-attention 。
 ◎ Attention机制
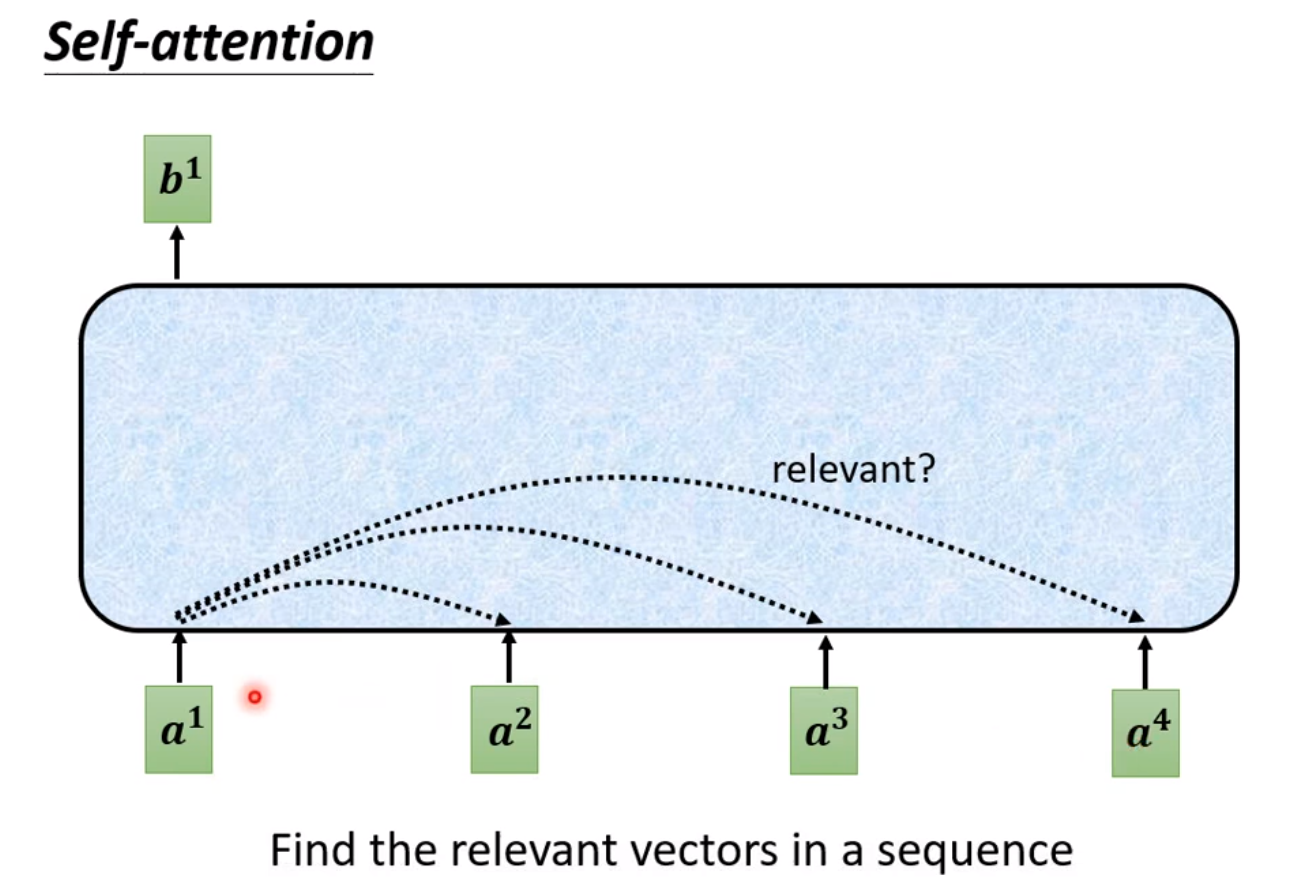
◎ Attention机制
Attention 为每一个输入的向量与其他向量计算相关度,最后输出的向量是每个向量根据相关度的加权总和。
在 Attention 里有三个符号定义需要特别注意:
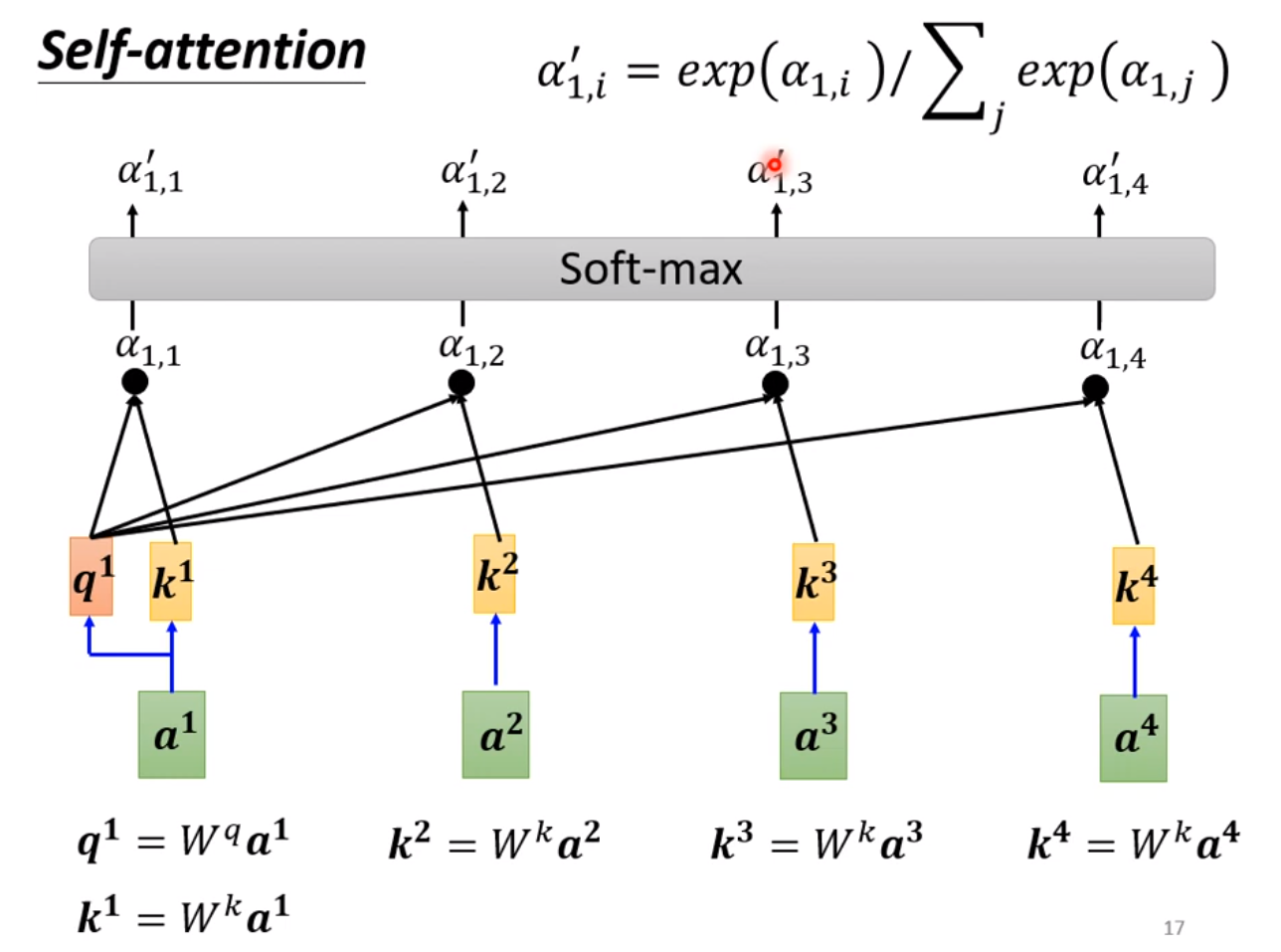
上面的小写 $q, k, v$ 指的是某个向量,可以认为 $q$ 是当前的输入向量,$k$ 是要与 $q$ 计算相关度的向量, $v$ 是最后要根据相关度加权求和对应的向量,它们的矩阵形式(即多个向量的集合) 用$Q, K, V$ 表示。
举个例子,上图的更具体的表示形式如下:
 ◎ q和k求相关度
◎ q和k求相关度
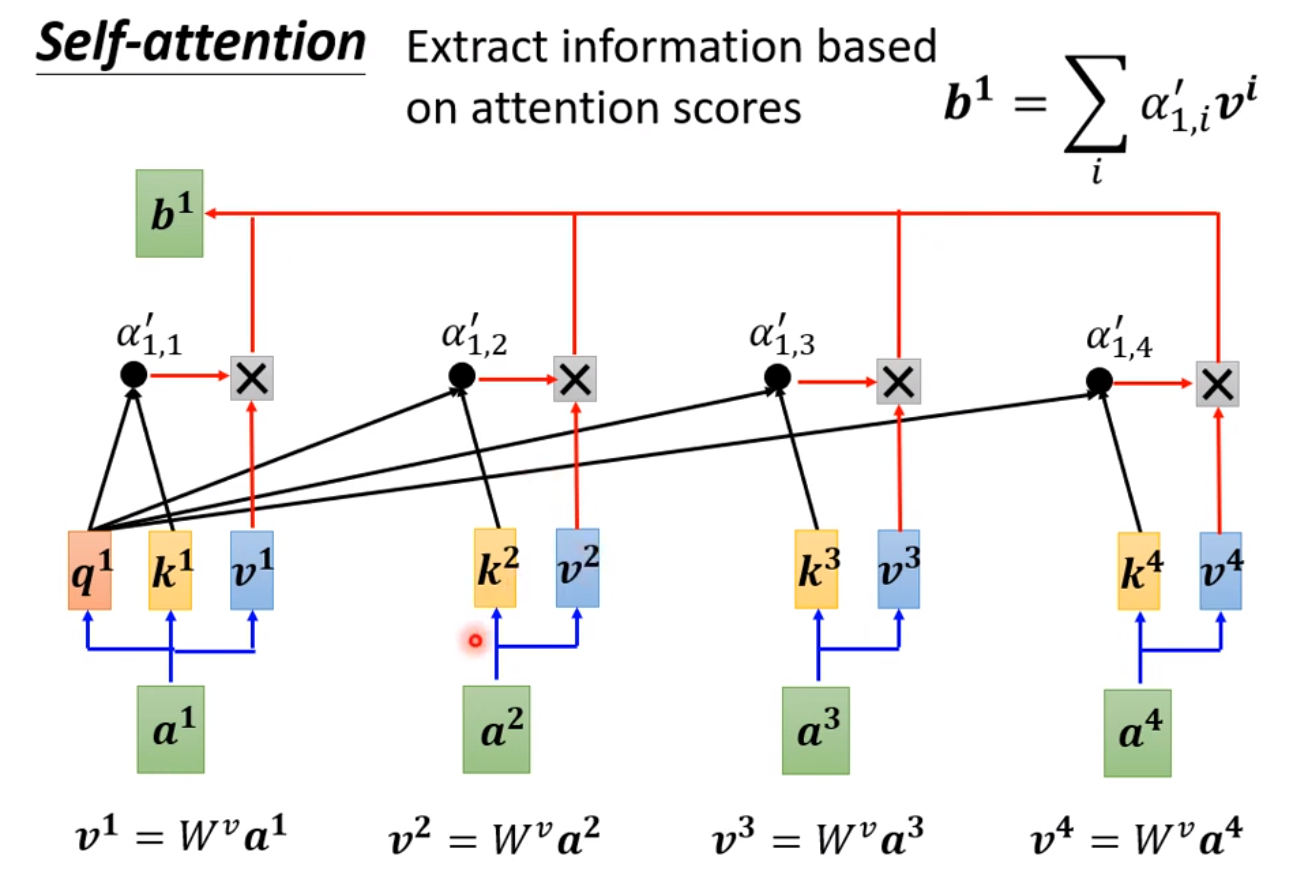 ◎ 根据相关度对v加权求和,得到新的向量
◎ 根据相关度对v加权求和,得到新的向量
对于输入的每一个向量都可以表示成上述的计算过程,很明显上述的过程对于多个输入向量是可以并行计算,这意味着可以表示成矩阵的形式。
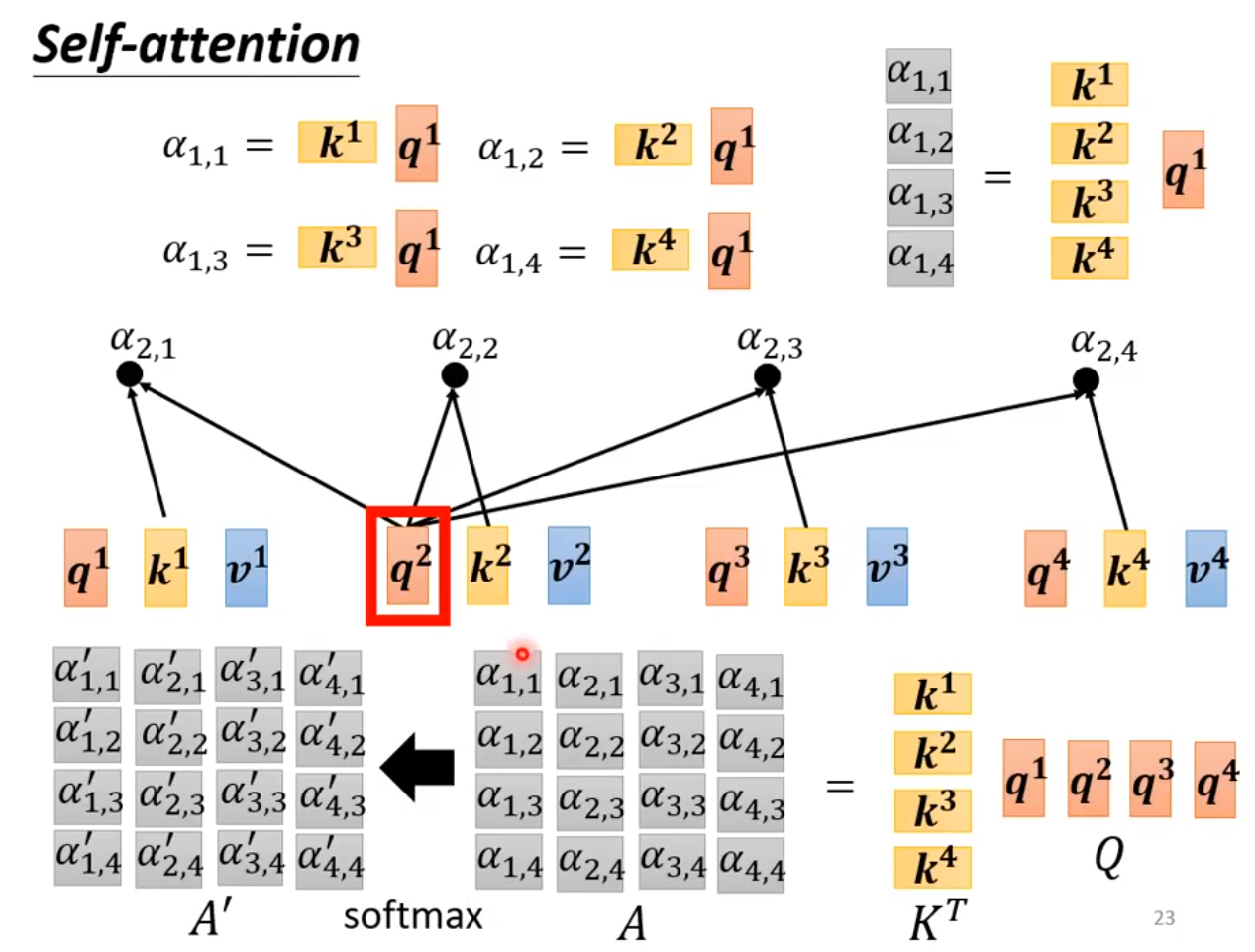 ◎ [q1, q2...]和 [k1, k2...]求相关度
◎ [q1, q2...]和 [k1, k2...]求相关度
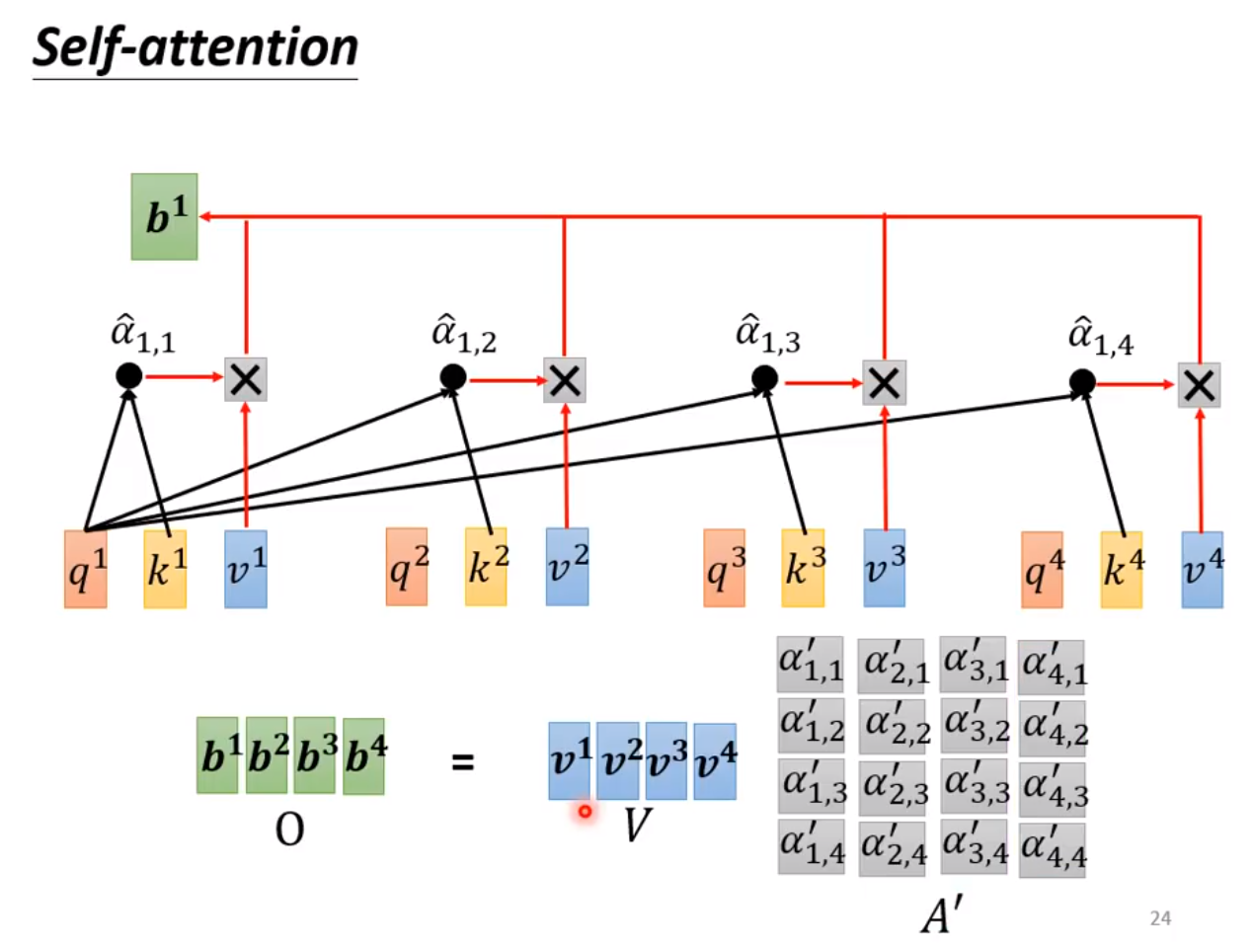 ◎ 根据相关度对v加权求和,得到新的向量, 并行输出多个新向量[b1, b2...]
◎ 根据相关度对v加权求和,得到新的向量, 并行输出多个新向量[b1, b2...]
用矩阵的形式表示 $Q, K, V$ 的计算过程如下:
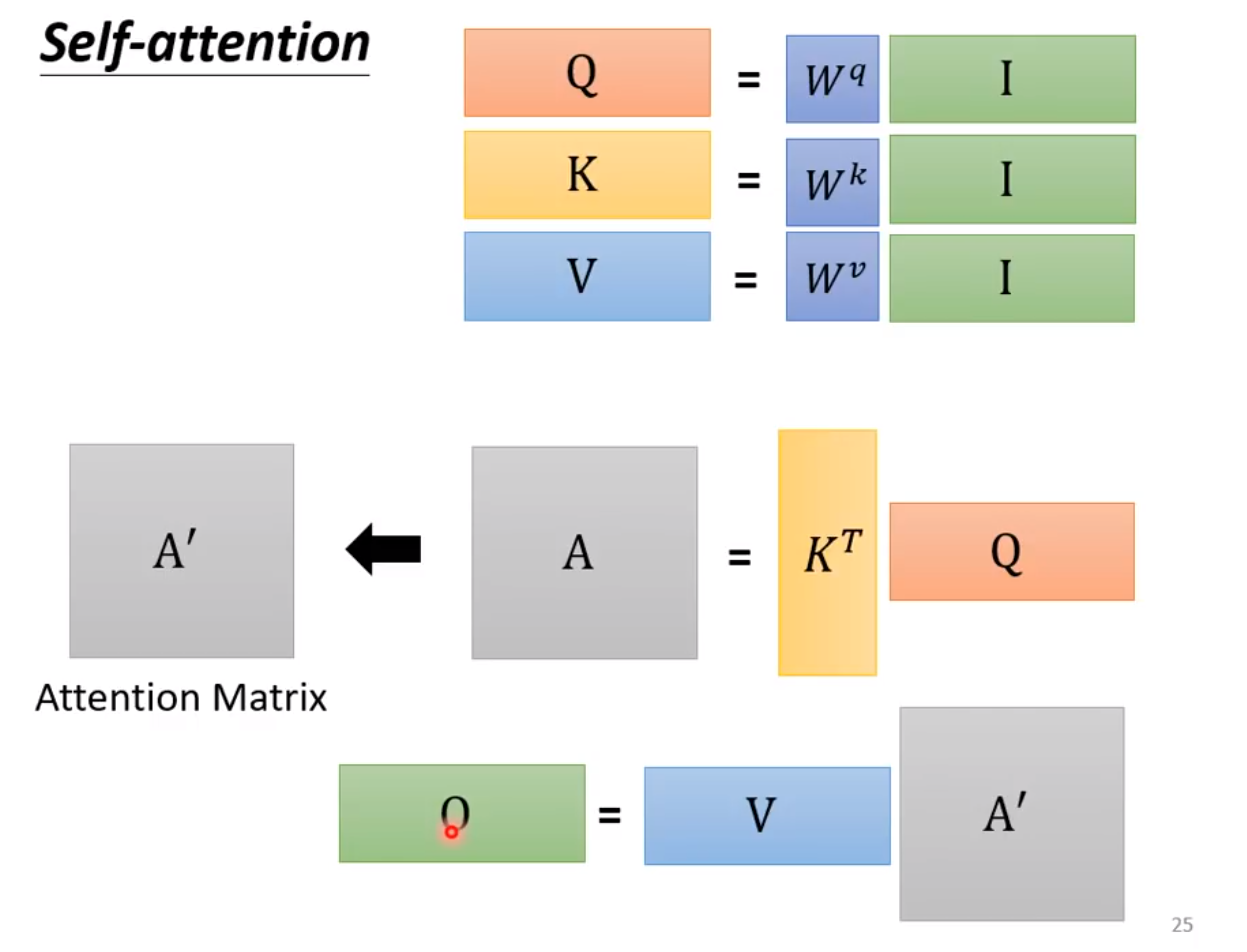 ◎ 用矩阵的形式表示
◎ 用矩阵的形式表示
在上图中,
$$
\boldsymbol{I} \in\mathbb{R}^{d_i\times n}
$$
$$
\boldsymbol{Q}\in\mathbb{R}^{d_k\times n}, \boldsymbol{K}\in\mathbb{R}^{d_k\times m}, \boldsymbol{V}\in\mathbb{R}^{d_v\times m}
$$
$$
\boldsymbol{O} = V \times k^T \times Q \in\mathbb{R}^{d_v\times n}
$$
更规范的公式表达是:
$$
\begin{equation}Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = softmax\left(\frac{\boldsymbol{Q}\boldsymbol{K}^{\top}}{\sqrt{d_k}}\right)\boldsymbol{V}\end{equation}
$$
其中 除以维度的平方根 $\sqrt{d_k}$ ,目的是使得$K, V$内积的结果不至于太大。
Attention可以分为Self-attention 和 Cross-attention, 在Self-attention中,$Q$ 和 $K, V$ 属于同一个向量序列, 在Cross-attention中,$Q$ 和 $K, V$ 属于不同向量序列。
Multi-head Self-attention 就是把 $Q,K,V$ 通过参数矩阵映射一下,然后再做 Attention ,把这个过程重复做n次,结果拼接起来,再经过一层线性变换做维度变换, 用于表示不同类型的相关性。
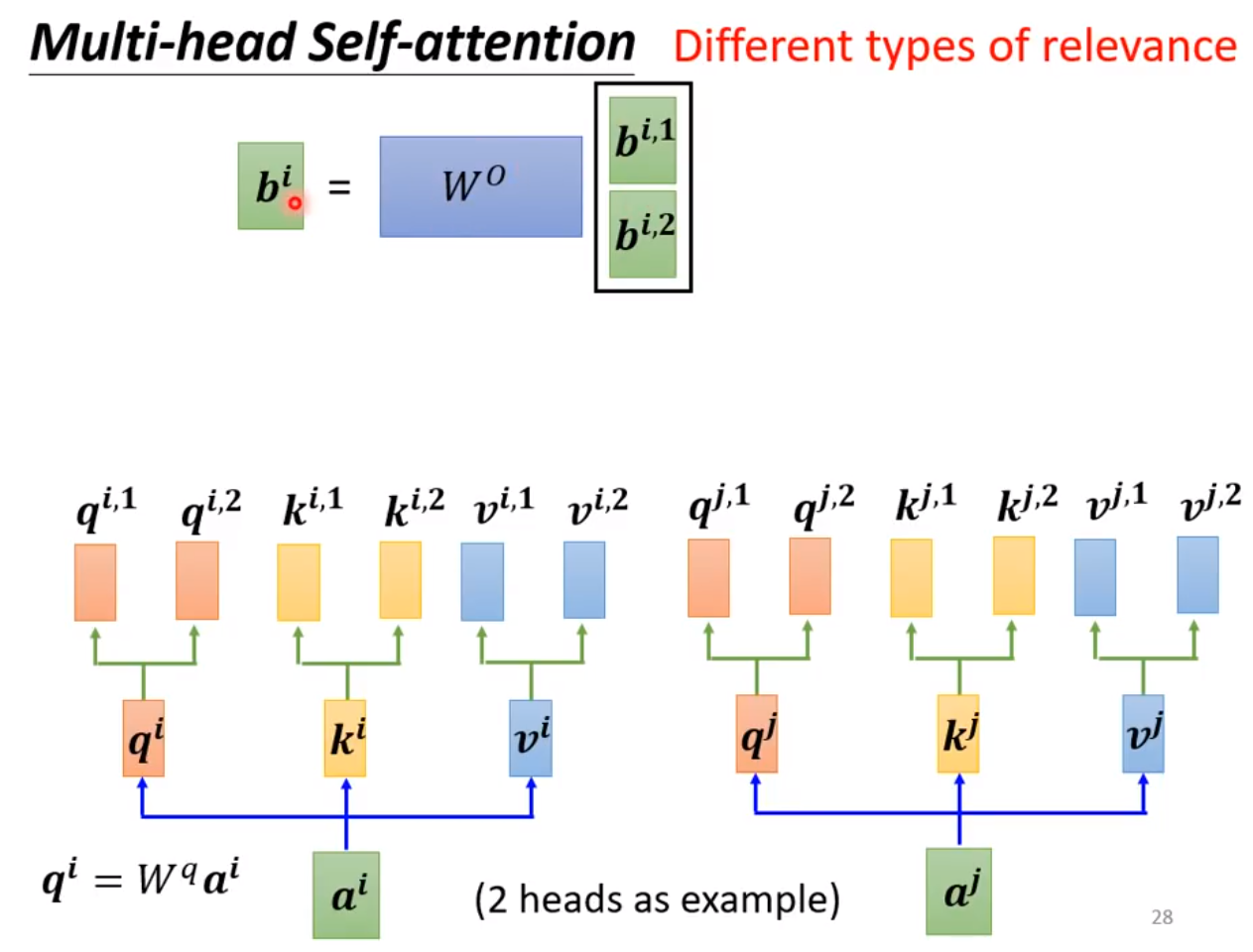 ◎ Multi-head Self-attention
◎ Multi-head Self-attention
上面是对 Attention 结构的简单介绍,严谨的符号定义还是得看原论文。
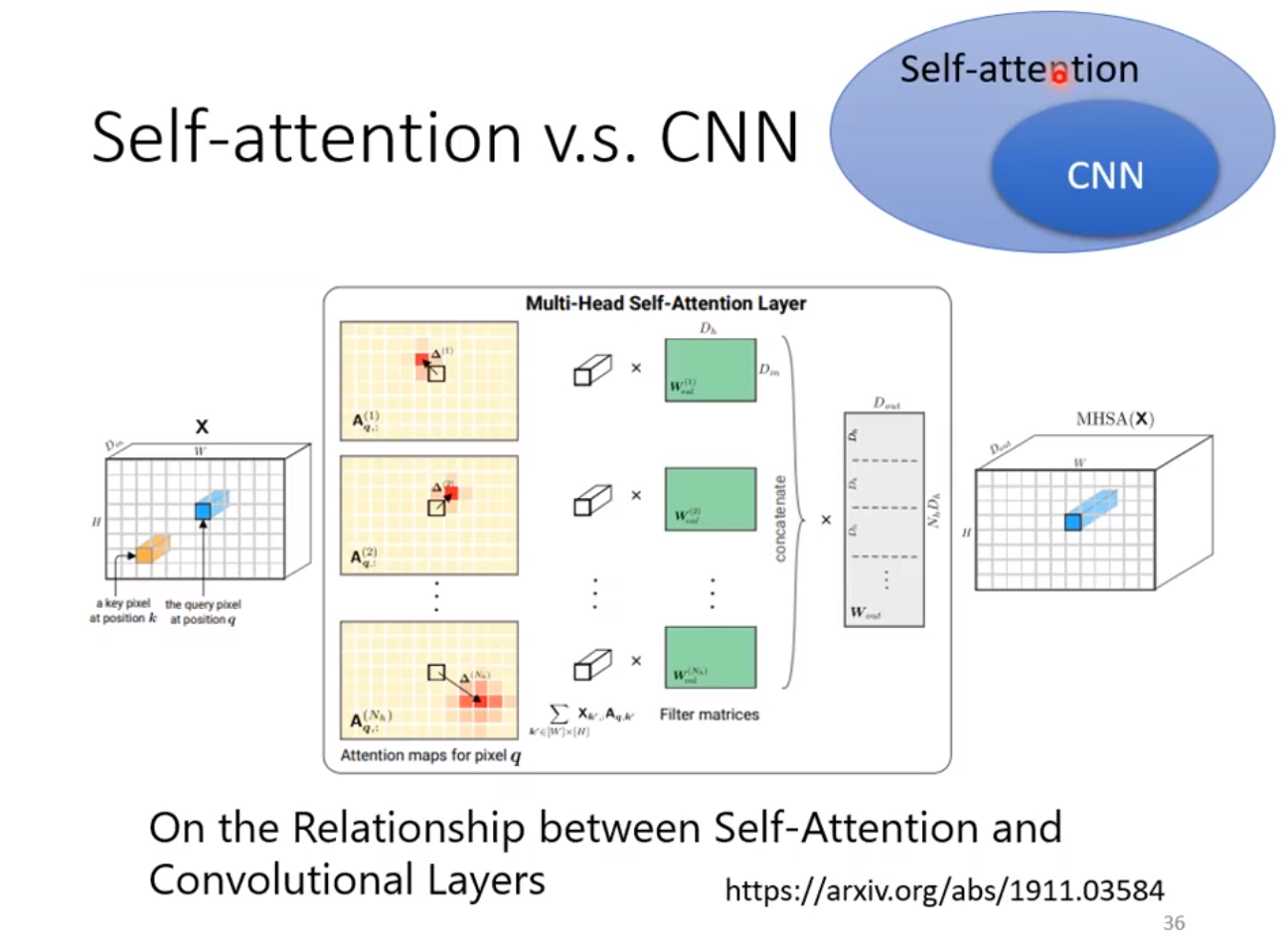 ◎ CNN是Attention的特殊表达形式
◎ CNN是Attention的特殊表达形式
Attention 用过计算相关性来加权融合不同的向量得到新的向量, 可以看作是更加灵活的CNN。CNN可以当做是Attention的子集,在论文On the Relationship between Self-Attention and Convolutional Layers有具体的论证。
可以注意到上面计算的相关性矩阵和GNN中的节点邻接矩阵很相似,向量集合$V$根据$Q, K$算出来的相关性矩阵加权求和的过程和图节点根据邻接矩阵做特征汇聚也是相似的,感兴趣的可以去进一步了解 Attention 和 GNN 的联系。
下面是对 Transformer 的编码层和解码层的介绍。
我们来看Transformer的编码层是怎么实现的:
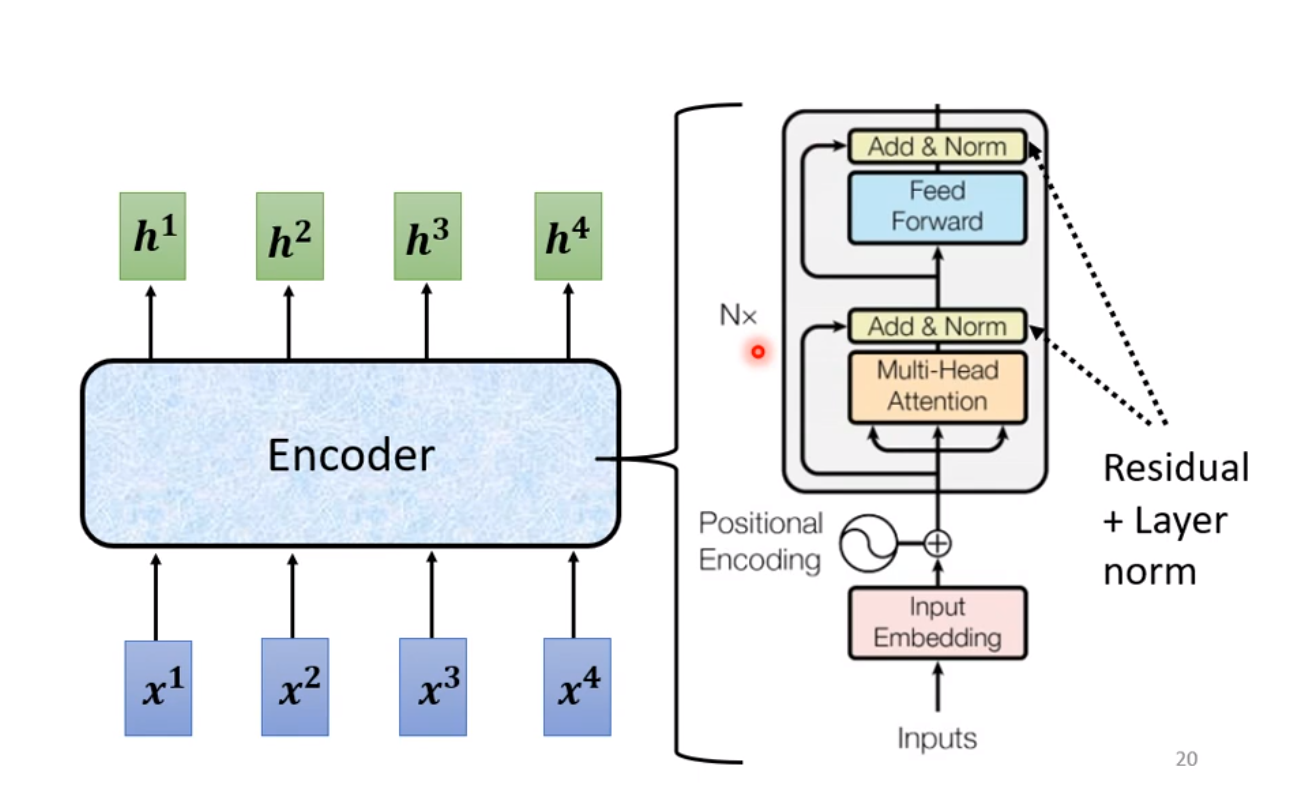 ◎ Encoder示意图
◎ Encoder示意图
有几个需要注意的细节:
- Input Embedding
Input Embedding 是将输入转化为向量集合的方式,对于不同的任务处理方法不同。Positional Encoding 的作用是使得到的嵌入向量带有位置信息,这对于一些位置相关的任务是至关重要的。
Positional Encoding 可以用手工的方式设计:
$$
PE_{2i}(p)=\sin\Big(p/10000^{2i/{d_{pos}}}\Big)
$$
$$
PE_{2i+1}(p)=\cos\Big(p/10000^{2i/{d_{pos}}}\Big)
$$
这里的意思是将$id$为$p$的位置映射为一个$d_{pos}$维的位置向量,这个向量的第$i$个元素的数值就是$PE_i(p)$。
这里采用正余弦函数的设计是为了让位置编码能反应相对的位置信息。比如已知$p$的位置信息, $p+d$的位置信息,由正余弦公式展开:
$$
\sin(p+d)=\sin p \cos d + \cos p \sin d
$$
和
$$
\cos(p+d)=\cos p \cos d - \sin p \sin d
$$
已知绝对位置$p$和相对位置$d$, 可以得到 $p+d$ 的绝对信息表示。
当然还有其他的位置编码方法,比如设计网络从数据中学习得到编码信息。
- Muiti-Head Attention
指的是上文说过的做 Muiti-Head Self-Attention 的过程
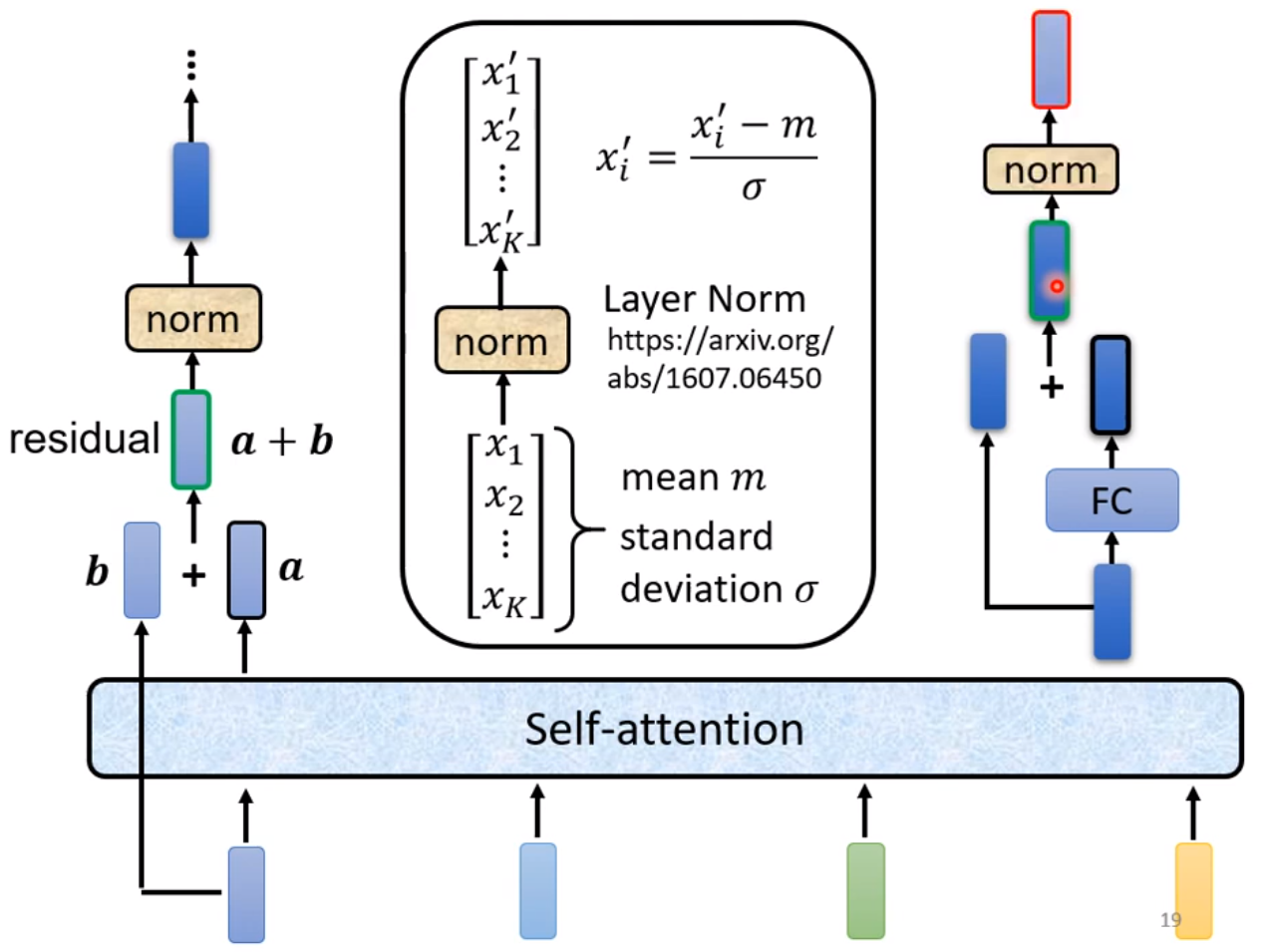 ◎ Encoder更多细节
◎ Encoder更多细节
- Add add Norm
Add 指的是 residual 结构,这在很多经典网络架构中都涉及到。Norm 指的是 Layer Norm ,对每一个向量求元素的均值和方差做归一化。这个和 Batch Norm 有所区别:Batch Norm 指的是在一个批次的数据中,对相同维度的元素做归一化。
- Feed Forward
经过多层全连接层构成前馈网络, 做维度的变换,进一步提高网络的表示能力。
上述的 Muiti-Head Attention-->Add add Norm-->Feed Forward-->Add add Norm会重复 $N$次。
解码层,首先输入一个标志位,结合编码器的编码信息输出第一个解码信息,联合标志位和第一个解码信息作为输入,结合结合编码器的编码信息输出第二个解码信息...以此类推。
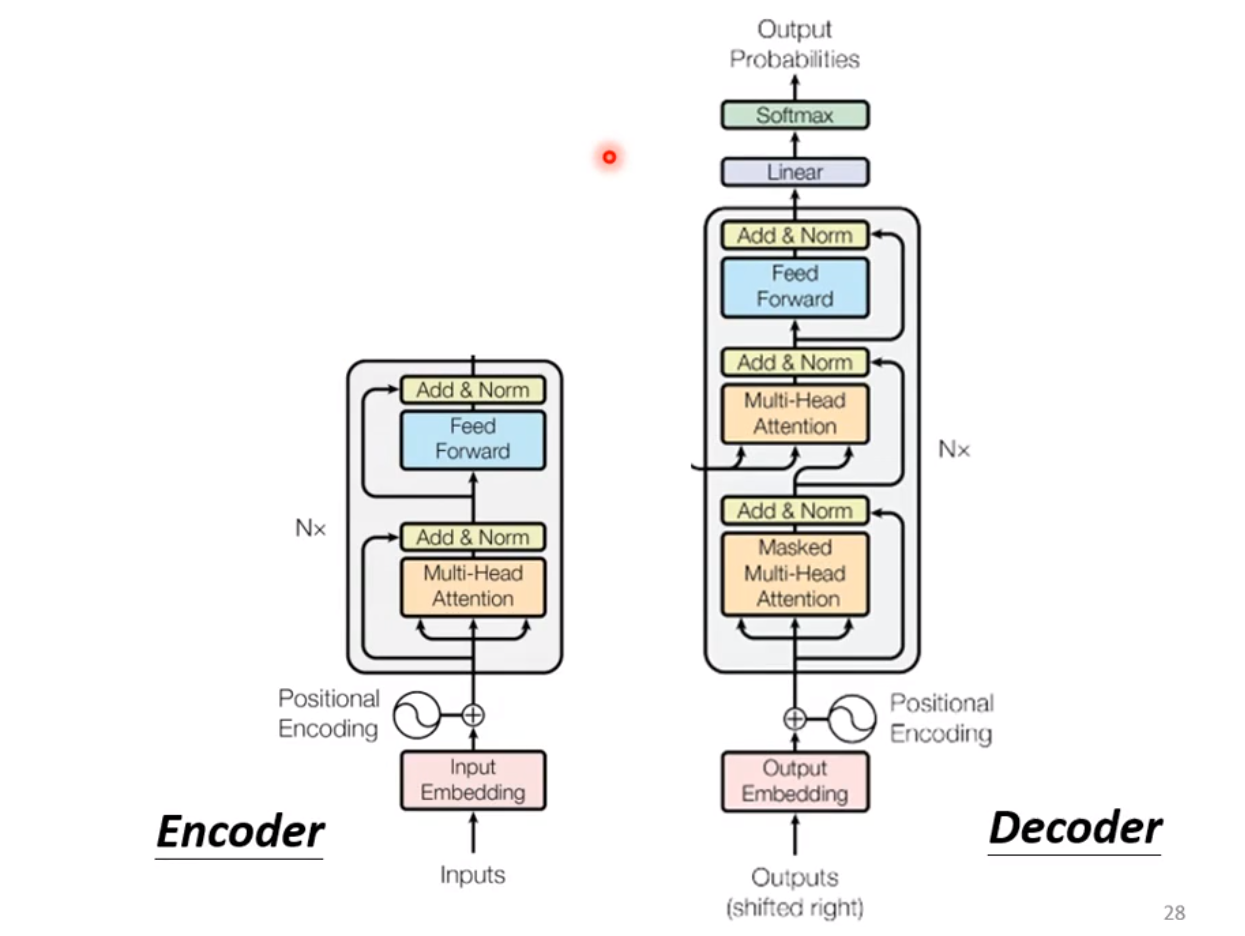 ◎ Decoder模块
◎ Decoder模块
值得注意的几点:
- Masked-Multi-Head Attention
带有Mask的 Multi-Head Self-Attention, 因为在解码阶段的输入不可能预先知道解码后的输出是什么,所以需要设置一个 Mask (下三角矩阵), 把为输出的解码位信息遮盖。
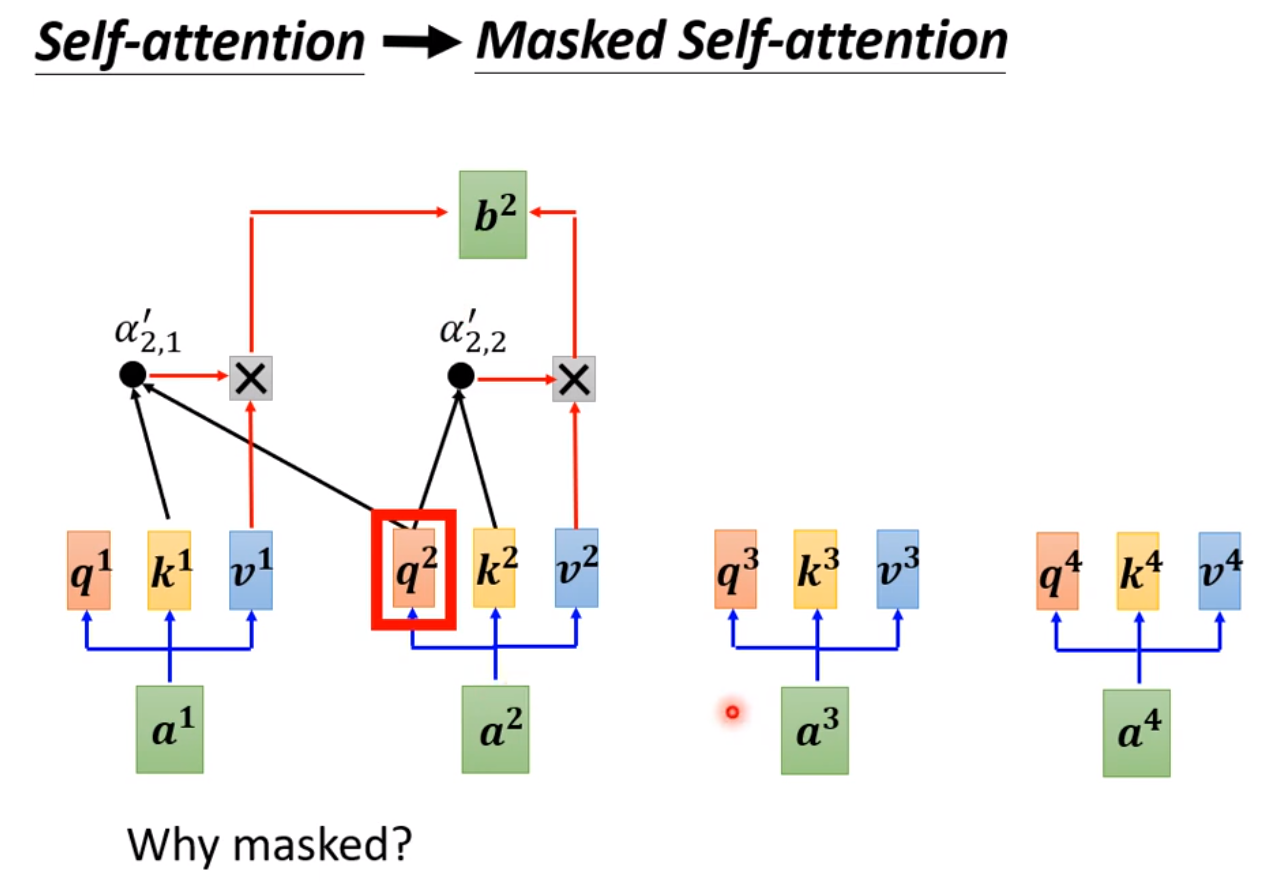 ◎ Masked-Multi-Head Attention
◎ Masked-Multi-Head Attention
- 第二个 Multi-Head Attention
这里其实是 Multi-Head Cross-Attention ,其中 $Q$ 来自解码器输入, $K, V$ 来自编码器最后一层的输出。
- 解码过程什么时候停止
可以在训练的时候,训练标签中当解码器的输入属于最后一个输入,则输出一个结束符,让网络在数据中自行学习什么时候停止。这属于AT Decoder,(AT 指的是auto termination), 也有一些 NAT Decoder 的方法,一次性并行输入$N$个标志位, 一次性输出解码信息。
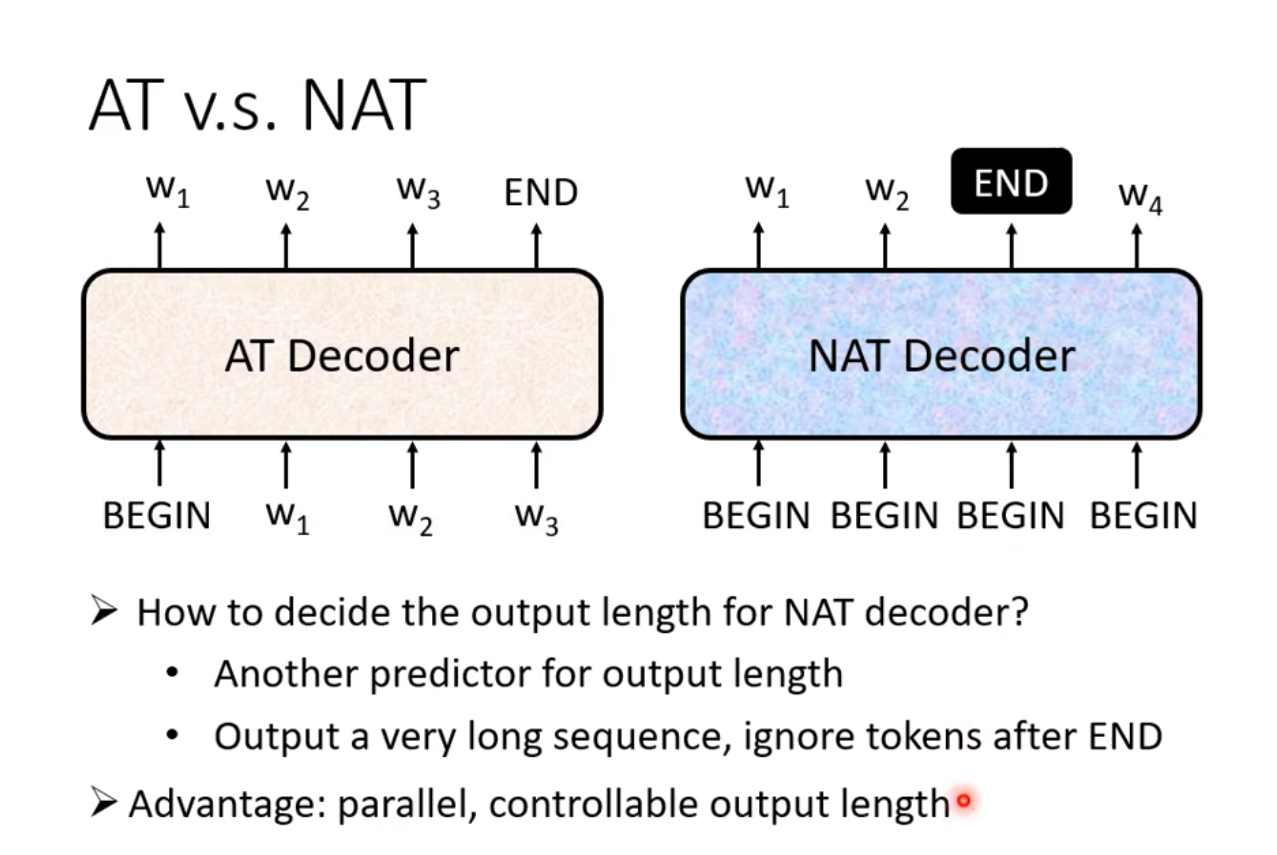 ◎ AT and NAT
◎ AT and NAT
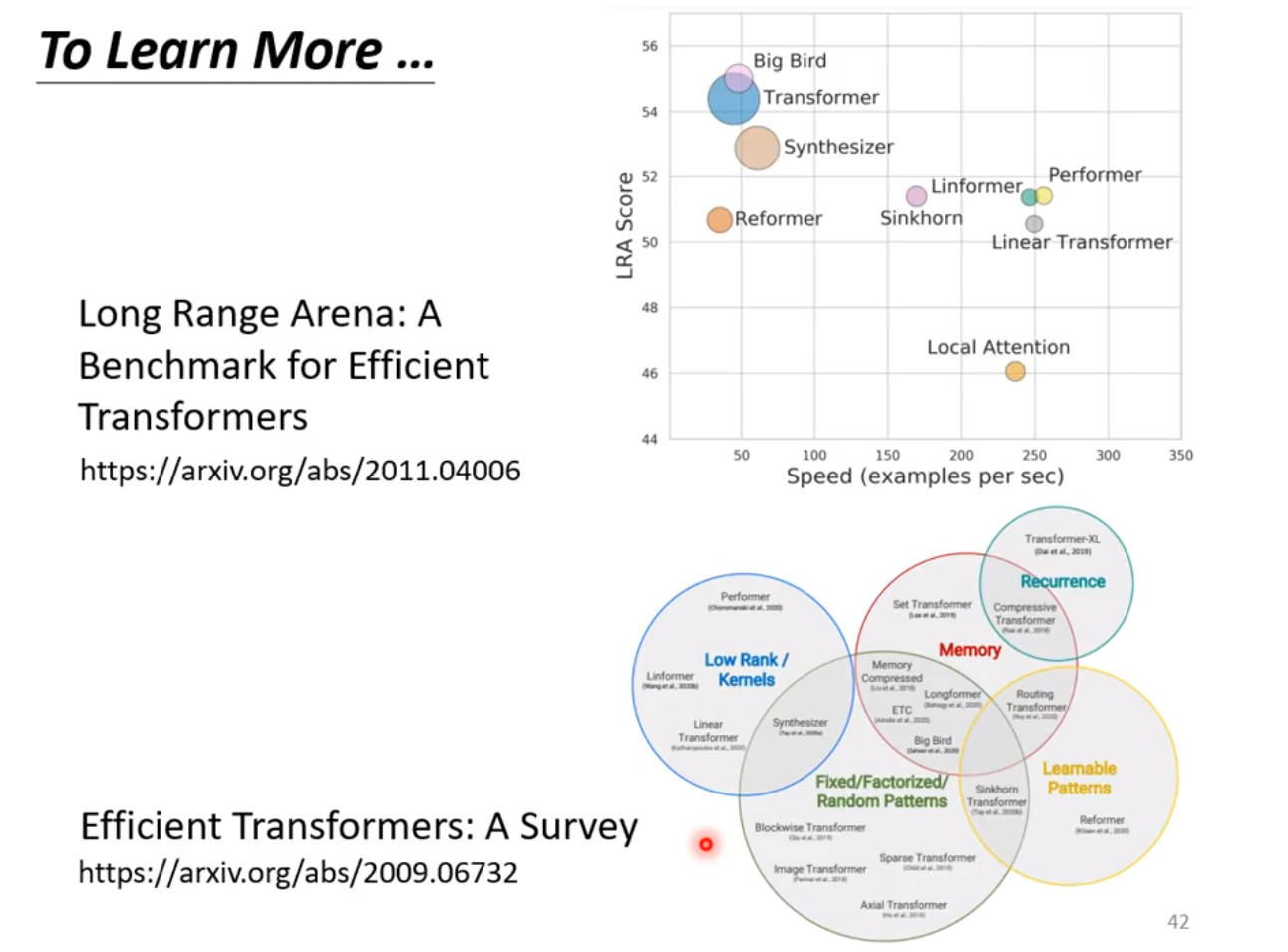 ◎ 更多的结构变式
◎ 更多的结构变式
代码参考3W字长文带你轻松入门视觉transformer
1
2
3
4
5
6
7
8
9
10
|
def get_position_angle_vec(position):
# hid_j是0-511,d_hid是512,position表示单词位置0~N-1
return [position / np.power(10000, 2 * (hid_j // 2) / d_hid) for hid_j in range(d_hid)]
# 每个单词位置0~N-1都可以编码得到512长度的向量
sinusoid_table = np.array([get_position_angle_vec(pos_i) for pos_i in range(n_position)])
# 偶数列进行sin, 间隔是2
sinusoid_table[:, 0::2] = np.sin(sinusoid_table[:, 0::2]) # dim 2i
# 奇数列进行cos, 间隔是2
sinusoid_table[:, 1::2] = np.cos(sinusoid_table[:, 1::2]) # dim 2i+1
|
可以看作是一个输入$X$ 分别经过多个Self-attention后再级联起来,最后通过线性变换改变输出维度。
单个 Self-attention 实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class ScaledDotProductAttention(nn.Module):
''' Scaled Dot-Product Attention '''
def __init__(self, temperature, attn_dropout=0.1):
super().__init__()
self.temperature = temperature
self.dropout = nn.Dropout(attn_dropout)
def forward(self, q, k, v, mask=None):
# self.temperature是论文中的d_k ** 0.5,防止梯度过大
# QxK/sqrt(dk)
attn = torch.matmul(q / self.temperature, k.transpose(2, 3))
if mask is not None:
# 屏蔽不想要的输出
attn = attn.masked_fill(mask == 0, -1e9)
# softmax+dropout
attn = self.dropout(F.softmax(attn, dim=-1))
# 概率分布xV
output = torch.matmul(attn, v)
return output, attn
|
 ◎ 再看编码层的结构
◎ 再看编码层的结构
下面的代码实现 Multi-head Self-attention + Add and Norm的过程。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
class MultiHeadAttention(nn.Module):
''' Multi-Head Attention module '''
# n_head头的个数,默认是8
# d_model编码向量长度,例如本文说的512
# d_k, d_v的值一般会设置为 n_head * d_k=d_model,
# 此时concat后正好和原始输入一样,当然不相同也可以,因为后面有fc层
# 相当于将可学习矩阵分成独立的n_head份
def __init__(self, n_head, d_model, d_k, d_v, dropout=0.1):
super().__init__()
# 假设n_head=8,d_k=64
self.n_head = n_head
self.d_k = d_k
self.d_v = d_v
# d_model输入向量,n_head * d_k输出向量
# 可学习W^Q,W^K,W^V矩阵参数初始化
self.w_qs = nn.Linear(d_model, n_head * d_k, bias=False)
self.w_ks = nn.Linear(d_model, n_head * d_k, bias=False)
self.w_vs = nn.Linear(d_model, n_head * d_v, bias=False)
# 最后的输出维度变换操作
self.fc = nn.Linear(n_head * d_v, d_model, bias=False)
# 单头自注意力
self.attention = ScaledDotProductAttention(temperature=d_k ** 0.5)
self.dropout = nn.Dropout(dropout)
# 层归一化
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
def forward(self, q, k, v, mask=None):
# 假设qkv输入是(b,100,512),100是训练每个样本最大单词个数
# 一般qkv相等,即自注意力
residual = q
# 将输入x和可学习矩阵相乘,得到(b,100,512)输出
# 其中512的含义其实是8x64,8个head,每个head的可学习矩阵为64维度
# q的输出是(b,100,8,64),kv也是一样
q = self.w_qs(q).view(sz_b, len_q, n_head, d_k)
k = self.w_ks(k).view(sz_b, len_k, n_head, d_k)
v = self.w_vs(v).view(sz_b, len_v, n_head, d_v)
# 变成(b,8,100,64),方便后面计算,也就是8个头单独计算
q, k, v = q.transpose(1, 2), k.transpose(1, 2), v.transpose(1, 2)
if mask is not None:
mask = mask.unsqueeze(1) # For head axis broadcasting.
# 输出q是(b,8,100,64),维持不变,内部计算流程是:
# q*k转置,除以d_k ** 0.5,输出维度是b,8,100,100即单词和单词直接的相似性
# 对最后一个维度进行softmax操作得到b,8,100,100
# 最后乘上V,得到b,8,100,64输出
q, attn = self.attention(q, k, v, mask=mask)
# b,100,8,64-->b,100,512
q = q.transpose(1, 2).contiguous().view(sz_b, len_q, -1)
# 线性变换
q = self.dropout(self.fc(q))
# Add: 残差计算
q += residual
# Norm: 层归一化,在512维度计算均值和方差,进行层归一化
q = self.layer_norm(q)
return q, attn
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class PositionwiseFeedForward(nn.Module):
''' A two-feed-forward-layer module '''
def __init__(self, d_in, d_hid, dropout=0.1):
super().__init__()
# 两个fc层,对最后的512维度进行变换
self.w_1 = nn.Linear(d_in, d_hid) # position-wise
self.w_2 = nn.Linear(d_hid, d_in) # position-wise
self.layer_norm = nn.LayerNorm(d_in, eps=1e-6)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
residual = x
x = self.w_2(F.relu(self.w_1(x)))
x = self.dropout(x)
x += residual
x = self.layer_norm(x)
return x
|
Transformer 的编码层是上述的结构的反复堆叠,单层编码层如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class EncoderLayer(nn.Module):
def __init__(self, d_model, d_inner, n_head, d_k, d_v, dropout=0.1):
super(EncoderLayer, self).__init__()
self.slf_attn = MultiHeadAttention(n_head, d_model, d_k, d_v, dropout=dropout)
self.pos_ffn = PositionwiseFeedForward(d_model, d_inner, dropout=dropout)
def forward(self, enc_input, slf_attn_mask=None):
# Q K V是同一个,自注意力
# enc_input来自源单词嵌入向量或者前一个编码器输出
enc_output, enc_slf_attn = self.slf_attn(
enc_input, enc_input, enc_input, mask=slf_attn_mask)
enc_output = self.pos_ffn(enc_output)
return enc_output, enc_slf_attn
|
注意的是:除了第一个模块输入是单词嵌入向量与位置编码的和外,其余编码层输入是上一个编码器输出即后面的编码器输入不需要位置编码向量。
完整的n个编码器如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Encoder(nn.Module):
def __init__(
self, n_src_vocab, d_word_vec, n_layers, n_head, d_k, d_v,
d_model, d_inner, pad_idx, dropout=0.1, n_position=200):
# nlp领域的词嵌入向量生成过程(单词在词表里面的索引idx-->d_word_vec长度的向量)
self.src_word_emb = nn.Embedding(n_src_vocab, d_word_vec, padding_idx=pad_idx)
# 位置编码
self.position_enc = PositionalEncoding(d_word_vec, n_position=n_position)
self.dropout = nn.Dropout(p=dropout)
# n个编码器层
self.layer_stack = nn.ModuleList([
EncoderLayer(d_model, d_inner, n_head, d_k, d_v, dropout=dropout)
for _ in range(n_layers)])
# 层归一化
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
def forward(self, src_seq, src_mask, return_attns=False):
# 对输入序列进行词嵌入,加上位置编码
enc_output = self.dropout(self.position_enc(self.src_word_emb(src_seq)))
enc_output = self.layer_norm(enc_output)
# 作为编码器层输入
for enc_layer in self.layer_stack:
enc_output, _ = enc_layer(enc_output, slf_attn_mask=src_mask)
return enc_output
|
 ◎ 再看解码器结构
◎ 再看解码器结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class DecoderLayer(nn.Module):
''' Compose with three layers '''
def __init__(self, d_model, d_inner, n_head, d_k, d_v, dropout=0.1):
super(DecoderLayer, self).__init__()
self.slf_attn = MultiHeadAttention(n_head, d_model, d_k, d_v, dropout=dropout)
self.enc_attn = MultiHeadAttention(n_head, d_model, d_k, d_v, dropout=dropout)
self.pos_ffn = PositionwiseFeedForward(d_model, d_inner, dropout=dropout)
def forward(
self, dec_input, enc_output,
slf_attn_mask=None, dec_enc_attn_mask=None):
# 标准的自注意力,QKV=dec_input来自目标单词嵌入或者前一个解码器输出
dec_output, dec_slf_attn = self.slf_attn(
dec_input, dec_input, dec_input, mask=slf_attn_mask)
# KV来自最后一个编码层输出enc_output,Q来自带有mask的self.slf_attn输出
dec_output, dec_enc_attn = self.enc_attn(
dec_output, enc_output, enc_output, mask=dec_enc_attn_mask)
dec_output = self.pos_ffn(dec_output)
return dec_output, dec_slf_attn, dec_enc_attn
|
n个Decoder的堆叠如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Decoder(nn.Module):
def __init__(
self, n_trg_vocab, d_word_vec, n_layers, n_head, d_k, d_v,
d_model, d_inner, pad_idx, n_position=200, dropout=0.1):
# 目标单词嵌入
self.trg_word_emb = nn.Embedding(n_trg_vocab, d_word_vec, padding_idx=pad_idx)
# 位置嵌入向量
self.position_enc = PositionalEncoding(d_word_vec, n_position=n_position)
self.dropout = nn.Dropout(p=dropout)
# n个解码器
self.layer_stack = nn.ModuleList([
DecoderLayer(d_model, d_inner, n_head, d_k, d_v, dropout=dropout)
for _ in range(n_layers)])
# 层归一化
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
def forward(self, trg_seq, trg_mask, enc_output, src_mask, return_attns=False):
# 目标单词嵌入+位置编码
dec_output = self.dropout(self.position_enc(self.trg_word_emb(trg_seq)))
dec_output = self.layer_norm(dec_output)
# 遍历每个解码器
for dec_layer in self.layer_stack:
# 需要输入3个信息:目标单词嵌入+位置编码、最后一个编码器输出enc_output
# 和dec_enc_attn_mask,解码时候不能看到未来单词信息
dec_output, dec_slf_attn, dec_enc_attn = dec_layer(
dec_output, enc_output, slf_attn_mask=trg_mask, dec_enc_attn_mask=src_mask)
return dec_output
|
在第一层的 Decoder 仍然有位置编码层, 嵌入特征向量要右移一个单位,则第一个位置的输入是一个特殊符号表示解码开始。
比如分类问题: Linear + softmax:
1
2
3
|
self.trg_word_prj = nn.Linear(d_model, n_trg_vocab, bias=False)
dec_output, *_ = self.model.decoder(trg_seq, trg_mask, enc_output, src_mask)
return F.softmax(self.model.trg_word_prj(dec_output), dim=-1)
|
 ◎ LOFTR
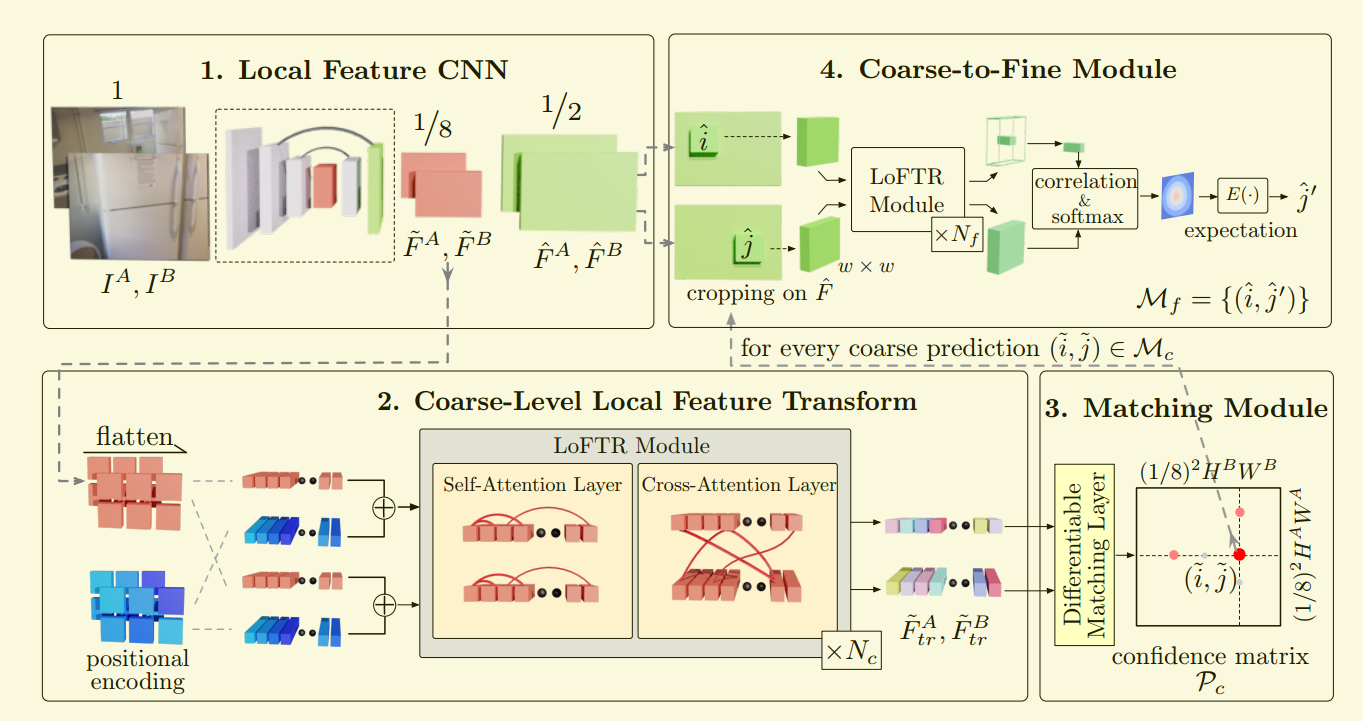
◎ LOFTR
LOFTR的处理流程如下:
-
用局部特征提取网络从图像$I_A$以及$I_B$中提取粗略特征图 $\tilde {F} ^ {A}$和$ \tilde {F} ^ {B}$,以及精细的特征图$ \hat {F} ^ {A} $和$ \hat {F} ^ {B} $。
-
将粗略特征图展平为一维向量,并添加位置编码;然后经过LoFTR 模块进行处理,则经过$N_c$个self-attention 和 cross-attention层的编码。
-
将可微分匹配层(softmax 或者匈牙利算法)用于匹配上述变换后的特征,最终得到置信矩阵 。根据置信度阈值和相互邻近标准选择匹配项,得到粗略的匹配预测 。
-
对于每个选定的粗略预测$(\tilde {i},\tilde {j})$ ,我们会从精细特征图中裁剪出具有大小为 $w \times w$的局部窗口。粗匹配将在此局部窗口内进行细化为并达到亚像素匹配级别,作为最终的匹配预测。
下面是LOFTR中与Transformer相关的模块代码:
由于是处理图像信息,位置编码是在$x, y$两个维度都进行位置编码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class PositionEncodingSine(nn.Module):
"""
This is a sinusoidal position encoding that generalized to 2-dimensional images
"""
def __init__(self, d_model, max_shape=(256, 256)):
"""
Args:
max_shape (tuple): for 1/8 featmap, the max length of 256 corresponds to 2048 pixels
"""
super().__init__()
pe = torch.zeros((d_model, *max_shape))
y_position = torch.ones(max_shape).cumsum(0).float().unsqueeze(0)
x_position = torch.ones(max_shape).cumsum(1).float().unsqueeze(0)
div_term = torch.exp(torch.arange(0, d_model//2, 2).float() * (-math.log(10000.0) / d_model//2))
div_term = div_term[:, None, None] # [C//4, 1, 1]
pe[0::4, :, :] = torch.sin(x_position * div_term)
pe[1::4, :, :] = torch.cos(x_position * div_term)
pe[2::4, :, :] = torch.sin(y_position * div_term)
pe[3::4, :, :] = torch.cos(y_position * div_term)
# self.register_buffer('pe', pe.unsqueeze(0), persistent=False) # [1, C, H, W]
self.pe = torch.unsqueeze(pe,0).cuda()
def forward(self, x):
"""
Args:
x: [N, C, H, W]
"""
return x + self.pe[:, :, :x.size(2), :x.size(3)]
|
self-transformer和cross-transformer交叠使用:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
|
class LoFTREncoderLayer(nn.Module):
def __init__(self,
d_model,
nhead,
attention='linear'):
super(LoFTREncoderLayer, self).__init__()
self.dim = d_model // nhead
self.nhead = nhead
# multi-head attention
self.q_proj = nn.Linear(d_model, d_model, bias=False)
self.k_proj = nn.Linear(d_model, d_model, bias=False)
self.v_proj = nn.Linear(d_model, d_model, bias=False)
self.attention = LinearAttention() if attention == 'linear' else FullAttention()
# multi-head输出的线性融合
self.merge = nn.Linear(d_model, d_model, bias=False)
# feed-forward network
self.mlp = nn.Sequential(
nn.Linear(d_model*2, d_model*2, bias=False),
nn.ReLU(True),
nn.Linear(d_model*2, d_model, bias=False),
)
# norm and dropout
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
def forward(self, x, source, x_mask:Optional[torch.Tensor], source_mask:Optional[torch.Tensor]) -> torch.Tensor:
"""
Args:
x (torch.Tensor): [N, L, C]
source (torch.Tensor): [N, S, C]
x_mask (torch.Tensor): [N, L] (optional)
source_mask (torch.Tensor): [N, S] (optional)
"""
bs = x.size(0)
query, key, value = x, source, source
# multi-head attention
query = self.q_proj(query).view(bs, -1, self.nhead, self.dim) # [N, L, (H, D)]
key = self.k_proj(key).view(bs, -1, self.nhead, self.dim) # [N, S, (H, D)]
value = self.v_proj(value).view(bs, -1, self.nhead, self.dim)
message = self.attention(query, key, value, q_mask=x_mask, kv_mask=source_mask) # [N, L, (H, D)]
message = self.merge(message.view(bs, -1, self.nhead*self.dim)) # [N, L, C]
message = self.norm1(message)
# feed-forward network
message = self.mlp(torch.cat([x, message], dim=2))
message = self.norm2(message)
# 这里稍微和原本的transformer不一样
return x + message
class LocalFeatureTransformer(nn.Module):
"""A Local Feature Transformer (LoFTR) module."""
def __init__(self, config):
super(LocalFeatureTransformer, self).__init__()
self.config = config
self.d_model = config['d_model']
self.nhead = config['nhead']
self.layer_names = config['layer_names']
encoder_layer = LoFTREncoderLayer(config['d_model'], config['nhead'], config['attention'])
self.layers = nn.ModuleList([copy.deepcopy(encoder_layer) for _ in range(len(self.layer_names))])
self._reset_parameters()
def _reset_parameters(self):
for p in self.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p)
def forward(self, feat0, feat1, mask0:Optional[torch.Tensor], mask1:Optional[torch.Tensor])->Tuple[torch.Tensor, torch.Tensor]:
"""
Args:
feat0 (torch.Tensor): [N, L, C]
feat1 (torch.Tensor): [N, S, C]
mask0 (torch.Tensor): [N, L] (optional)
mask1 (torch.Tensor): [N, S] (optional)
"""
assert self.d_model == feat0.size(2), "the feature number of src and transformer must be equal"
for idx, v in enumerate(self.layers):
name = self.layer_names[idx];
layer = v;
if name == 'self':
feat0 = layer(feat0, feat0, mask0, mask0)
feat1 = layer(feat1, feat1, mask1, mask1)
elif name == 'cross':
feat0 = layer(feat0, feat1, mask0, mask1)
feat1 = layer(feat1, feat0, mask1, mask0)
else:
raise KeyError
return feat0, feat1
|
ViT 和 DETR在3W字长文带你轻松入门视觉transformer中有详细介绍和代码注释。
 ◎ ViT
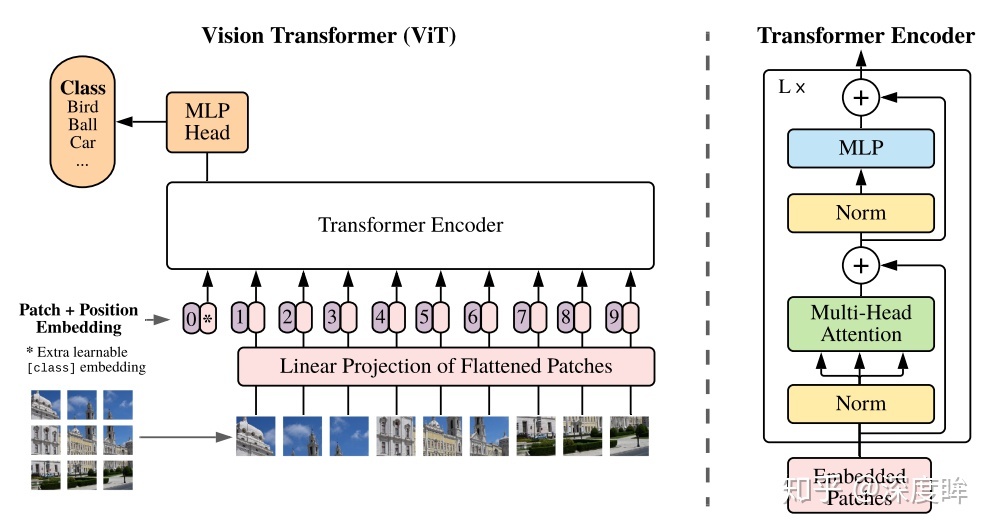
◎ ViT
ViT将图像切块构建嵌入向量,并只用Transformer中的编码器模块实现图像分类, 在 ViT中,作者在嵌入向量集合的最开始添加了一个属于可学习参数的嵌入向量, 并将该输入对应的输出向量用于图像分类(如果不加入这个向量,用剩下其他的输出向量中的哪个都说不过去,不过我觉得可以将输出经过一个线性变换后,再用于分类)。
 ◎ DETR
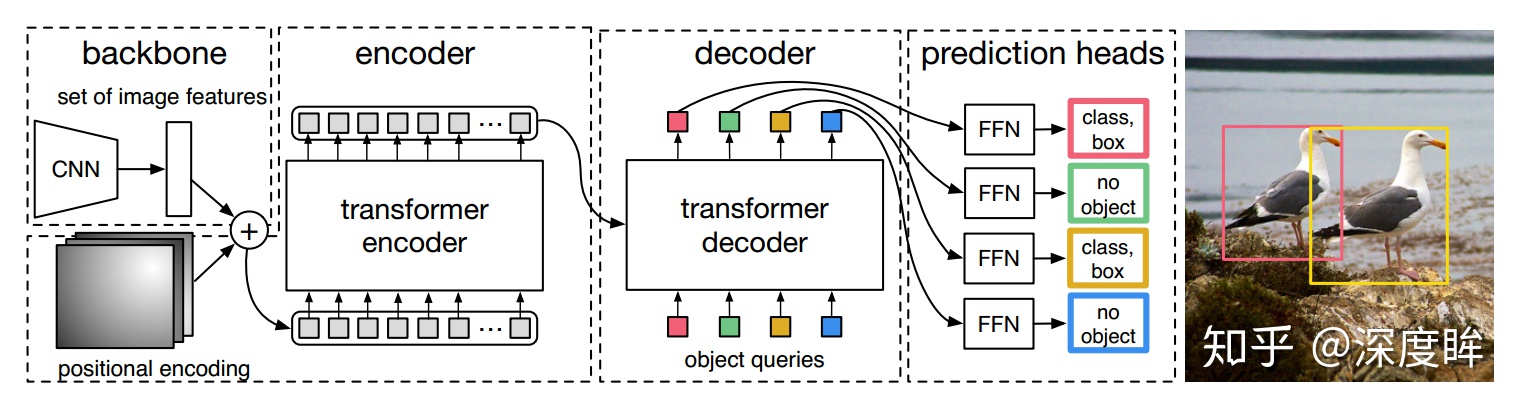
◎ DETR
而 DETR 是将 Transformer 用于目标检测。它的每一层编码器和解码器都添加位置编码信息,而且解码器的输入是前面说的 NAT 方式,一次性输入初始化全0的(100,b,256)的输出嵌入向量,经过多层解码器后,将最后一个解码器输出输入到分类和回归head中,得到100个无序集合,再后处理得到提取前景类别和对应的bbox坐标。
最近出了两篇视觉Transformer的综述文章,感兴趣的可以进一步去了解:
- 华为等提出视觉Transformer:全面调研
- 又一篇视觉Transformer综述来了!
 ◎ Transformer
◎ Transformer ◎ 处理流程
◎ 处理流程 ◎ Attention机制
◎ Attention机制 ◎ q和k求相关度
◎ q和k求相关度 ◎ 根据相关度对v加权求和,得到新的向量
◎ 根据相关度对v加权求和,得到新的向量 ◎ [q1, q2...]和 [k1, k2...]求相关度
◎ [q1, q2...]和 [k1, k2...]求相关度 ◎ 根据相关度对v加权求和,得到新的向量, 并行输出多个新向量[b1, b2...]
◎ 根据相关度对v加权求和,得到新的向量, 并行输出多个新向量[b1, b2...] ◎ 用矩阵的形式表示
◎ 用矩阵的形式表示 ◎ Multi-head Self-attention
◎ Multi-head Self-attention ◎ CNN是Attention的特殊表达形式
◎ CNN是Attention的特殊表达形式 ◎ Encoder示意图
◎ Encoder示意图 ◎ Encoder更多细节
◎ Encoder更多细节 ◎ Decoder模块
◎ Decoder模块 ◎ Masked-Multi-Head Attention
◎ Masked-Multi-Head Attention ◎ AT and NAT
◎ AT and NAT ◎ 更多的结构变式
◎ 更多的结构变式 ◎ 再看编码层的结构
◎ 再看编码层的结构 ◎ 再看解码器结构
◎ 再看解码器结构 ◎ LOFTR
◎ LOFTR ◎ ViT
◎ ViT ◎ DETR
◎ DETR