基于图匹配的平面匹配算法

在人类感知的尺度上，平面是人类社会环境中最常见的结构之一，并且具有强大的约束能力，约束着大量的点/线及其所携带的信息。各种曲面都可以用平面进行近似，根据精度要求选择拟合的平面数量。实际应用中，许多计算机视觉任务都需要平面信息，比如：机器人领域中，识别地面、墙面等平面可用于路径规划、视觉导航，识别桌面、书架等平面可辅助机械手抓取和放置物品；增强现实、混合现实中，利用平面信息放置物品，或者更换桌面、地板、墙面的纹理可以进行快速展示；三维场景重建中，用平面而非点云可以实现对一个城市大规模、简洁的重建。

整个流程主要分成三个模块：

1. 平面提取
2. 提取平面特征构建特征描述子
3. 利用图匹配的方法匹配平面

平面提取

基于单张彩色图输入的平面提取任务旨在从图像中分割出所拍摄场景中的平面结构，并同时估计相机到平面的深度信息。

基于单张彩色图输入的平面提取首先是从图片中提取特征。传统方法关注的是几何基元的提取，比如点、线段等；也会使用纹理信息，比如颜色、形状等。神经网络强大的特征提取能力可以从像素点中提取信息，然后聚合成平面；也有研究是用神经网络提取图片中点、线之类的几何基元来构成平面。

几何方法

几何方法提取平面使用一种自下而上的方法，即先寻找单张彩色图片中的几何基 元来 恢 复 三 维 信 息，从 而 进 一 步 提 取 平面。为了提高平面提取精度，大部分几何方法使用了一定的场景约束，最常用的是曼哈顿世界假设（曼哈顿世界假设是指场景中不同朝向的平面应相互正交，即分别对应三维笛卡尔坐标系中的ｘｙ面、ｘｚ面和ｙｚ 面。），这使得它们的应用场景也受到了极大得约束。

神经网络提取平面

神经网络提取平面的主要流程是利用现有的网络作为编码器对图片信息进行提取，然后通过几个分支将这些信息解码成平面/非平面掩膜、平面实例分割掩膜和深度图，最终整合为完整的3Ｄ 平面模型，流程图如下：

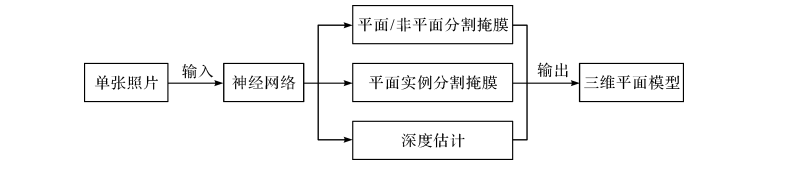
大部分文献通过聚合像素点来提取平面，主要思路是将平面提取问题转化为语义分割问题或实例 分割问题。也有文献在曼哈顿世界假设下，提取图片中的３Ｄ线框（wireframe）然后提取平面。此方法用直线和连接点组成平面，因此提取出的平面边缘整齐平滑，而聚合像素的方法提取出的平面边缘相对粗糙。但该方法相应地对边缘为曲线的平面提取效果较差。

本文采纳上图的思想，利用单张RGB图像估计平面/非平面掩膜、平面实例分割掩膜和深度图。由于在本文中，平面提取模块主要用于提取平面区域对应的特征构建平面特征描述子，故不涉及对平面三维信息的准确估计。(为提高平面特征描述子的表达能力，后面也尝试做了归一化深度的估计，但是否对描述子表达能力有促进作用还待实验证明)

关于平面提取还可以改善的地方

无论是何种方法，提取的平面边缘都存在一定问题：使用像素点聚合提取的平面边缘粗糙不平 滑，而通过直线段构成平面的方法对边缘为曲线的平面提取效果较差。基于单张彩色图输入的平面提取的未来工作主要是进一步提升平面分割和深度估计的精度。除此之外，还有很多拓展研究，比如：

1. 平面边缘的优化。如果平面由像素点构成，可对平面边缘进行平滑处理，或使用直线/曲线拟 合，或从图片中提取边缘信息后与平面的边缘结合。如果平面由线条构成，可以针对性地使用直线/曲线构成平面。

2. 遮挡推理。单张彩色图包含的信息有限，从中提取的平面会因遮挡而部分缺失，比如被桌子遮 挡的墙面。使用图片中已有的纹理对平面缺失处进行填充，可极大提高平面重建的完整性和观赏性。

3. 绝对深度。由于缺失深度的维度，根据单张图片重建出的三维模型与真实世界相差一个因子，即尺度。可以通过图片内特定物体的尺寸来确定绝对深度。

4. 几何方法和神经网络方法的结合。两类方法各有优缺点，后续工作可通过取长补短的方式结合 两类方法，有以下两种思路可供参考：一是，传统方法难以有效建模图像中的不规则线段等几何信息，因此通过神经网络预测图像中的灭点、线段的位置等能更有效的提取图片中的几何信息，进而用传统几何方法根据已知的几何结构实现更高效的平面提取；二 是，利用神经网络提取的特征点 （例 如SuperPoint）替代传统人工特征点，提取更具有描述性和重复性的特征，进行平面位置以及平面边缘的定位。

用实例分割提取平面

为了得到平面的特征表示，在本实验将神经网络(骨干网络选择Res101)作为编码器对图片信息进行提取，然后通过几个分支将这些信息解码成平面/非平面掩膜、平面实例分割掩膜和深度图。为了让网络推理速度更快，我没有采用如Mask-rcnn的两阶段法（即先回归锚框位置再实例分割），而是采用论文 ^[1]中的单阶段方法，首先通过编码器提取输入图像的高维信息，然后用三个解码器分别学习到平面/非平面掩膜，平面嵌入特征(Plane embeddings)以及深度信息。利用其中的平面嵌入特征和平面/非平面掩膜通过均值漂移(Mean Shift)聚类算法得到平面的分割实例。

Mean Shift聚类算法

由于在实际场景中的平面数不固定，一些受初始聚类中心数目影响的算法(例如K-Means，K-Means++)并不适用于处理聚类个数未知的情形，对此，有一些改进的算法如Mean Shift算法被提出。与K-Means算法一样，Mean Shift算法是基于聚类中心的聚类算法，不同的是，Mean Shift算法不需要事先制定类别个数k。

对于给定的 $d$ 维空间 $R^d$ 中的 $n$ 个样本点 $x_i,i=1,⋯,n$，对于其中的点 $x$， 定义 Mean Shift向量的基本形式为：

$$ M_h(x)=\frac{1}{k}\sum_{x_i\in S_h}(x_i-x) $$

其中，$S_h$ 指的是一个半径为h的高维球区域，如上图中的圆形区域。$S_h$ 的定义为：

$$ S_h(x)=(y \mid (y-x)( y-x)^T \leqslant h^2) $$

为了使得随着样本与被偏移点的距离不同，其偏移量对均值偏移向量的贡献也不同，需要在Mean Shift算法中引入核函数，此时改进的Mean Shift向量形式：

$$ M_h(x)=\frac{\sum_{i=1}^{n}G(\frac{x_i-x}{h_i})(x_i-x)}{\sum_{i=1}^{n}G(\frac{x_i-x}{h_i})} $$

其中， $$G(\frac{x_i-x}{h_i})$$ 为核函数(常见的核函数如高斯核函数，余弦函数等)。

计算 $M_h$ 时考虑距离的影响，同时也可以认为在所有的样本点 $X$ 中,重要性并不一样,因此对每个样本还引入一个权重系数。如此以来就可以把Mean Shift形式扩展为：

$$ M_h (x)=\frac{\sum_{i=1}^{n}G(\frac{x_i-x}{h_i})w(x_i)(x_i-x)}{\sum_{i=1}^{n}G(\frac{x_i-x}{h_i})w(x_i)} $$

其中，$w(x_i)$ 是一个赋给采样点的权重。

对于Mean Shift算法，它是一个迭代的步骤，即先算出当前点的偏移均值，将该点移动到此偏移均值，然后以此为新的起始点，继续移动，直到满足最终的条件。

Mean-Shift 聚类就是对于集合中的每一个元素，对它执行下面的操作：把该元素移动到它邻域中所有元素的特征值的均值的位置，不断重复直到收敛。准确的说，不是真正移动元素，而是把该元素与它的收敛位置的元素标记为同一类。

一般的均值漂移聚类会在每次迭代中对每个像素有 $N$ 次核函数的计算( $N$ 为像素总数)，计算复杂度是 $O(N^2)$ 。为了提高均值漂移聚类的效率，论文¹中生成 $k^d$ 个锚点，其中 $k$ 是每个维度的锚点数，$d$ 是嵌入特征的维度，然后仅仅计算 锚点与每个像素的核函数，计算复杂度是 $O(k^d \times N)$, 当 $k^d << N$ 时，算法执行效率大大提高。聚类完成后，论文¹再将小于设定阈值的锚点合并作为平面实例的聚类中心。

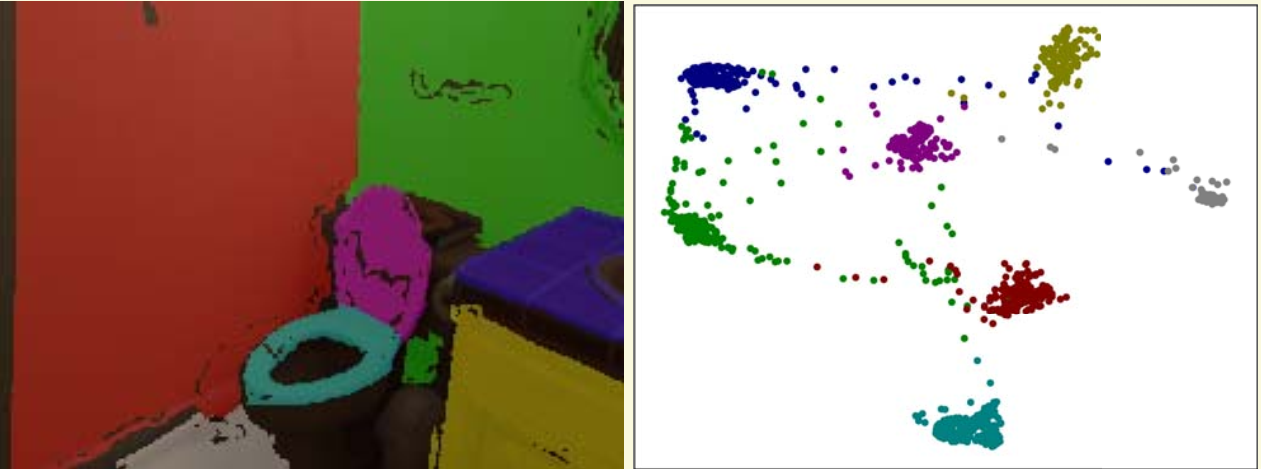◎ 应用均值漂移聚类后的像素分布示意图

文章链接

损失函数

• 平面/非平面掩膜的损失函数采用平衡交叉熵损失：

$$ L_{S}=-(1-w) \sum_{i \in \mathcal{F}} \log p_{i}-w \sum_{i \in \mathcal{B}} \log \left(1-p_{i}\right) $$

其中 $\mathcal{F}$ 和 $\mathcal{B}$ 是 前景和背景像素的集合， $p_i$ 是第 $i$ 个像素属于前景(平面)的概率， $w$ 是前景和背景的比率，是一个超参数。

• 嵌入特征的损失函数采用判别损失(discriminative loss),

该损失包括两部分：pull loss 和 push loss, pull loss将高维嵌入特征向聚类中心靠拢， push loss 使 聚类中心相互远离。

$$ L_{E}=L_{p u l l}+L_{p u s h} $$

其中：

$$ L_{\text {pull }}=\frac{1}{C} \sum_{c=1}^{C} \frac{1}{N_{c}} \sum_{i=1}^{N_{c}} \max \left(\left|\mu_{c}-x_{i}\right|-\delta_{\mathrm{v}}, 0\right) $$

$$ L_{\text {push }}=\frac{1}{C(C-1)} \sum_{c_{A}=1}^{C} \sum_{c_{B}=1}^{C} \max \left(\delta_{\mathrm{d}}-\left|\mu_{c_{A}}-\mu_{c_{B}}\right|,0\right). c_{A} \neq c_{B} $$

其中， $C$ 是聚类中心的个数（平面个数）， $N_c$ 是聚类区域 $c$ 中的元素数， $x_i$ 是 嵌入特征， $\mu_c$ 是聚类区域 $c$ 中的平均嵌入特征， $\delta_{\mathrm{v}}$ 和 $\delta_{\mathrm{d}}$ 是超参数。

• 深度图回归采用 Huber loss

$$ L_D = \operatorname{loss}(x, y)=\frac{1}{n} \sum_{i} z_{2} $$

其中

$$ z_{\imath}=0.5\left(x_{2}-y_{2}\right)^{2}, \text { if }\left|x_{2}-y_{i}\right|<1 $$

$$ z_{\imath}= \left|x_{\imath}-y_{\imath}\right|-0.5, \text { otherwise } $$

实验结果

第一二三四行依次为：平面分割结果， 平面分割和RGB图像混合结果， 平面/非平面掩模， 深度图。第一二三列依次为：原图， 网络预测结果， 真值。

提取平面特征构建特征描述子

构建图节点

在前面已经得到平面实例分割的前提下，对于每一个平面实例，选用一个矩形包围框，该包围框恰好能包含对应平面实例。然后用该包围框裁取前面特征提取网络编码器输出的深度嵌入特征区域以及对应的深度图对应区域，将两部分区域重采样到 $128 \times 128 \times N$， 其中 $N$ 是通道维数，对于深度嵌入特征，$N=64$， 对于深度图 $N=1$。

为了减低后续的网络的计算复杂度，提取的深度嵌入特征和深度图经过两次 max pooling 和一次 mean pooling， max pooling 同时还具有一定的抗平面旋转/平移的作用。

深度嵌入特征和深度图经过多层感知机(MLP)统一特征维度后级联在一起当做图网络的节点特征。

利用图匹配的方法匹配平面

两阶段图匹配算法

论文^[2] 中利用图内卷积和跨图卷积汇聚节点邻域特征，然后通过最优传输理论得到两个图之间的节点匹配关系，该方法由于将节点特征学习和全局匹配分开对待，因此网络运算效率不高；此外， 由于仅考虑局部嵌入，该方法可能倾向于不一致地匹配图之间的邻域。(邻域一致性保证邻域的节点不会匹配到待匹配图的不同区域)

论文^[3] 提出了一种完全可微分两阶段图匹配的方法，旨在由数据驱动解决 邻域一致的图节点匹配问题，而无需在网络推理阶段解决任何优化问题。

二阶段图匹配网络结构图如下所示：

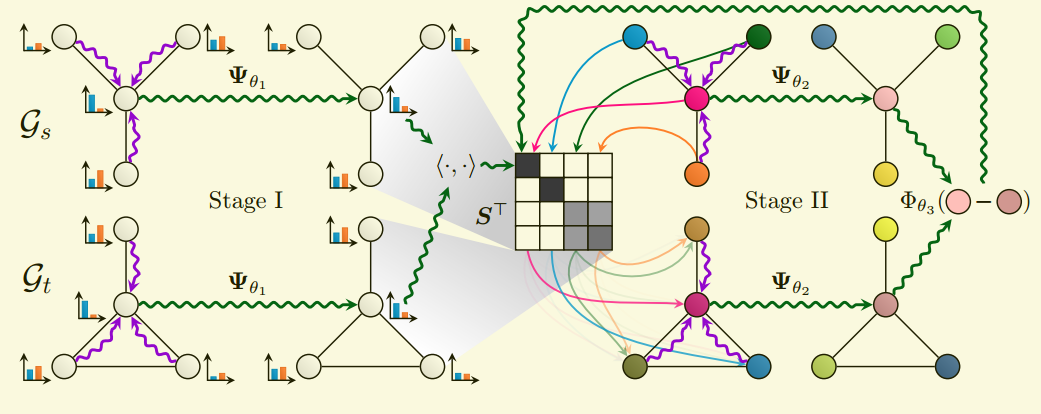◎ 二阶段图匹配网络

给定源图 $\mathcal{G}_{s}$ 和 目标图 $\mathcal{G}_{t}$, 首先通过GNN特征汇聚节点邻域特征, 即 $\boldsymbol{H}_{s}=\boldsymbol{\Psi}_{\theta_{1}}\left(\boldsymbol{X}_{s}, \boldsymbol{A}_{s}, \boldsymbol{E}_{s}\right) \in \mathbb{R}^{\left|\mathcal{V}_{s}\right| \times .}$ 和 $\boldsymbol{H}_{t}=\boldsymbol{\Psi}_{\theta_{1}}\left(\boldsymbol{X}_{t}, \boldsymbol{A}_{t}, \boldsymbol{E}_{t}\right) \in \mathbb{R}^{\left|\mathcal{V}_{t}\right| \times .}$, 其中 ${\Psi}_{\theta_{1}}$ 选用：

$$ \vec{h}_{i}^{(t+1)}= {\Psi}_{\theta_{1}}(\vec{h}_{i}^{(t)}) = \sigma\left(\boldsymbol{W}^{(t+1)} \vec{h}_{i}^{(t)}+\sum_{j \rightarrow i} \Phi_{\theta}^{(t+1)}\left(\vec{e}_{j, i}\right) \cdot \vec{h}_{j}^{(t)}\right) $$

这样，通过特征汇聚得到 $\boldsymbol{H}_{s}$ 和 $\boldsymbol{H}_{t}$ 后，通过矩阵行间的softmax 正则化后，计算源图和目标图的节点相似度，选取相似度最高的当做匹配节点，得到初始的匹配矩阵 $\boldsymbol{S}^{(0)}$。

损失函数：

$$ \mathcal{L}^{\text {(initial) }}=-\sum_{i \in \mathcal{V}_{s}} \log \left(S_{i, \pi_{\mathrm{gr}}(i)}^{(0)}\right) $$

其中 $\pi_{\mathrm{gr}}$ 是监督标签的目标图中与源图节点 $i$ 匹配的节点。

由于初始的匹配仅基于局部的匹配，网络有可能会让节点特征相似但不满足局部一致性的节点匹配上，这需要引入二阶段的匹配一致性学习。

对于二阶段的学习， 给定第 $l$ 次迭代时网络的匹配矩阵是 $S^{(l)}$, 通过共享权重的图网络 $\Psi_{\theta_{2}}$ 执行同步消息传递：

$$ \boldsymbol{O}_{s}=\boldsymbol{\Psi}_{\theta_{2}}\left(\boldsymbol{I}_{\left|\mathcal{V}_{s}\right|}, \boldsymbol{A}_{s}, \boldsymbol{E}_{s}\right) \quad \text { and } \quad \boldsymbol{O}_{t}=\boldsymbol{\Psi}_{\theta_{2}}\left(\boldsymbol{S}_{(l)}^{\top} \boldsymbol{I}_{\left|\mathcal{V}_{s}\right|}, \boldsymbol{A}_{t}, \boldsymbol{E}_{t}\right) $$

上面的 $\Phi_{\theta_{1}}$ 和 $\Phi_{\theta_{2}}$ 都采用相同的网络结构：

$$ \vec{h}_{i}^{(t+1)}=\sigma\left(\boldsymbol{W}^{(t+1)} \vec{h}_{i}^{(t)}+\sum_{j \rightarrow i} \Phi_{\theta}^{(t+1)}\left(\vec{e}_{j, i}\right) \cdot \vec{h}_{j}^{(t)}\right) $$

其中 $\Phi_{\theta}(.)$ 是关于边特征的可学习参数。

通过计算差值向量 $\vec{d}_{i, j}=\vec{o}_{i}^{(s)}-\vec{o}_{j}^{(t)}$ , 更新 匹配矩阵：

$$ S_{i, j}^{(l+1)}=\operatorname{softmax}\left(\hat{\boldsymbol{S}}^{(l+1)}\right)_{i, j} \text { with } \hat{S}_{i, j}^{(l+1)}=\hat{S}_{i, j}^{(l)}+\Phi_{\theta_{3}}\left(\vec{d}_{j, i}\right) $$

其中 $\Phi_{\theta_{3}}$ 是多层感知机。

网络的最终损失由特征匹配损失和邻域一致性损失构成：$\mathcal{L}=\mathcal{L}^{(\text {initial) }}+\mathcal{L}^{\text {(refined) }}$ with $\mathcal{L}^{\text {(refined) }}=-\sum_{i \in \mathcal{V}_{s}} \log \left(S_{i, \pi_{\mathrm{m}}(i)}^{(L)}\right)$ 。

实验结果

每张图第一第二行是匹配真值，第三四行是网络预测匹配结果。

参考文献