Python实现softmax回归分类

softmax回归模型概念

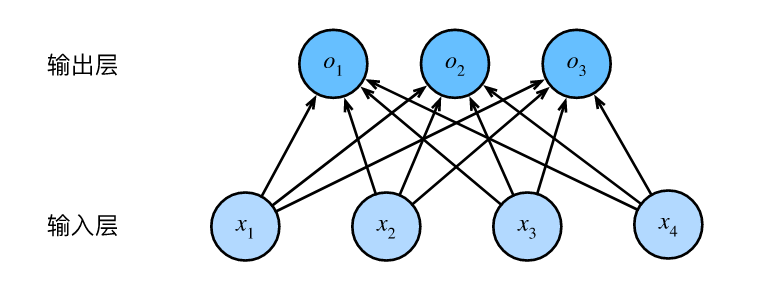
softmax回归跟线性回归一样将输入特征与权重做线性叠加。与线性回归的一个主要不同在于，softmax回归的输出值个数等于标签里的类别数。

数学模型

$$ \begin{aligned} o_1 &= x_1 w_{11} + x_2 w_{21} + x_3 w_{31} + x_4 w_{41} + b_1,\\ o_2 &= x_1 w_{12} + x_2 w_{22} + x_3 w_{32} + x_4 w_{42} + b_2,\\ o_3 &= x_1 w_{13} + x_2 w_{23} + x_3 w_{33} + x_4 w_{43} + b_3. \end{aligned} $$

若要输出是离散的预测，一个方法是取输出的最大值对应的类别作为预测输出（比如若输出是顺序排列的，则取输出最大值的下标做预测输出），则输出 $\operatorname*{argmax}_i o_i$。但为了使输出层的输出具有直观意义（例如表示概率值），先对网络输出用softmax运算符做归一化，将网络输出值变换成值为正且和为1的概率分布：

$$ \hat{y}_1, \hat{y}_2, \hat{y}_3 = \text{softmax}(o_1, o_2, o_3), $$

其中

$$ \hat{y}_1 = \frac{ \exp(o_1)}{\sum_{i=1}^3 \exp(o_i)},\quad \hat{y}_2 = \frac{ \exp(o_2)}{\sum_{i=1}^3 \exp(o_i)},\quad \hat{y}_3 = \frac{ \exp(o_3)}{\sum_{i=1}^3 \exp(o_i)}. $$

用矢量表示，定义：

$$ \boldsymbol{W} = \begin{bmatrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ w_{31} & w_{32} & w_{33} \\ w_{41} & w_{42} & w_{43} \end{bmatrix},\quad \boldsymbol{b} = \begin{bmatrix} b_1 & b_2 & b_3 \end{bmatrix}, $$ 样本i的特征为： $$ \boldsymbol{x}^{(i)} = \begin{bmatrix}x_1^{(i)} & x_2^{(i)} & x_3^{(i)} & x_4^{(i)}\end{bmatrix}, $$ 输出层的输出为： $$ \boldsymbol{o}^{(i)} = \begin{bmatrix}o_1^{(i)} & o_2^{(i)} & o_3^{(i)}\end{bmatrix}, $$ 最终的预测概率为： $$ \boldsymbol{\hat{y}}^{(i)} = \begin{bmatrix}\hat{y}_1^{(i)} & \hat{y}_2^{(i)} & \hat{y}_3^{(i)}\end{bmatrix}. $$

则softmax回归对样本$i$分类的矢量计算表达式为

$$ \begin{aligned} \boldsymbol{o}^{(i)} &= \boldsymbol{x}^{(i)} \boldsymbol{W} + \boldsymbol{b},\\ \boldsymbol{\hat{y}}^{(i)} &= \text{softmax}(\boldsymbol{o}^{(i)}). \end{aligned} $$

以上是单样本的矢量表示，若对小批量的矢量表示如下：

给定一个小批量样本，其批量大小为$n$，输入个数（特征数）$d$，输出个数（类别数）为$q$。设批量特征为$\boldsymbol{X} \in \mathbb{R}^{n \times d}$。假设softmax回归的权重和偏差参数分别为$\boldsymbol{W} \in \mathbb{R}^{d \times q}$和$\boldsymbol{b} \in \mathbb{R}^{1 \times q}$。softmax回归的矢量计算表达式为

$$ \begin{aligned} \boldsymbol{O} &= \boldsymbol{X} \boldsymbol{W} + \boldsymbol{b},\\ \boldsymbol{\hat{Y}} &= \text{softmax}(\boldsymbol{O}), \end{aligned} $$

网络结构

softmax网络模型和线性回归一样，依然是单层全连接层网络，可具体看下面的代码。

交叉熵损失函数

有了网络的输出$\boldsymbol{\hat{y}}^{(i)}$（是一组概率值）和真实标签$\boldsymbol{y}^{(i)}$，利用交叉熵损失函数计算损失值$l$。

$$ H(\boldsymbol y^{(i)}, \boldsymbol {\hat y}^{(i)} ) = -\sum_{j=1}^q y_j^{(i)} \log \hat y_j^{(i)}, $$

对于一个样本只有一个标签的情况，由于每个样本的标签中只有一个值为1，其他为0，上式可简化为

$$ H(\boldsymbol y^{(i)}, \boldsymbol {\hat y}^{(i)}) = -\log \hat y_{y^{(i)}}^{(i)} $$

假设训练数据集的样本数为$n$，交叉熵损失函数定义为 $$ \ell(\boldsymbol{\Theta}) = \frac{1}{n} \sum_{i=1}^n H\left(\boldsymbol y^{(i)}, \boldsymbol {\hat y}^{(i)}\right ), $$

优化算法

和线性回归一样，依然是小批量随机梯度下降，具体看下面的代码。

代码实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

import d2lzh as d2l
from mxnet import autograd, nd
from matplotlib import pyplot as plt

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

num_inputs = 784
num_outputs = 10

W = nd.random.normal(scale=0.01, shape=(num_inputs, num_outputs))
b = nd.zeros(num_outputs)
W.attach_grad()
b.attach_grad()

def softmax(X):
    X_exp = X.exp()
    partition = X_exp.sum(axis=1, keepdims=True) #对一行元素求和
    return X_exp / partition  # 这里应用了广播机制

def net(X):
    return softmax(nd.dot(X.reshape((-1, num_inputs)), W) + b) #n*784

def cross_entropy(y_hat, y):
    return -nd.pick(y_hat, y).log()

def accuracy(y_hat, y):
    return (y_hat.argmax(axis=1) == y.astype('float32')).mean().asscalar()

def evaluate_accuracy(data_iter, net):
    acc_sum, n = 0.0, 0
    for X, y in data_iter:
        y = y.astype('float32')
        acc_sum += (net(X).argmax(axis=1) == y).sum().asscalar()  #net(X).argmax(axis=1)返回一行中最大概率值对应的下标索引
        n += y.size
    return acc_sum / n

num_epochs, lr = 10, 0.1

# 本函数已保存在d2lzh包中方便以后使用
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
              params=None, lr=None, trainer=None):
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_iter:
            with autograd.record():
                y_hat = net(X)
                l = loss(y_hat, y).sum()
            l.backward()
            if trainer is None:
                d2l.sgd(params, lr, batch_size)
            else:
                trainer.step(batch_size)  # “softmax回归的简洁实现”一节将用到
            y = y.astype('float32')
            train_l_sum += l.asscalar()
            train_acc_sum += (y_hat.argmax(axis=1) == y).sum().asscalar()
            n += y.size
        test_acc = evaluate_accuracy(test_iter, net)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
              % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))

train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, batch_size,
          [W, b], lr)