模型欠拟合和过拟合

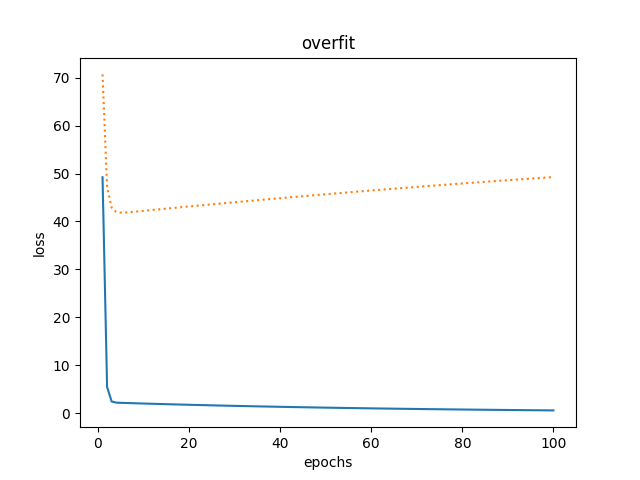
记录模型欠拟合和过拟合的原因和实验现象。摘自《动手学深度学习》

网络欠拟合和过拟合

概念

在讨论欠拟合和过拟合之前首先需要区分几个概念：

1 . 训练误差和泛化误差

训练误差（training error）和泛化误差（generalization error）。前者指模型在训练数据集上表现出的误差，后者指模型在任意一个测试数据样本上表现出的误差的期望，并常常通过测试数据集上的误差来近似。由于无法从训练误差估计泛化误差，一味地降低训练误差并不意味着泛化误差一定会降低。

2 . 模型选择

在机器学习中，通常需要评估若干候选模型的表现并从中选择模型。这一过程称为模型选择（model selection）。可供选择的候选模型可以是有着不同超参数的同类模型。以多层感知机为例，我们可以选择隐藏层的个数，以及每个隐藏层中隐藏单元个数和激活函数。

3 . 验证数据集

从严格意义上讲，测试集只能在所有超参数和模型参数选定后使用一次。不可以使用测试数据选择模型，如调参。但由于无法从训练误差估计泛化误差，因此也不应只依赖训练数据选择模型。鉴于此，我们可以预留一部分在训练数据集和测试数据集以外的数据来进行模型选择。这部分数据被称为验证数据集，简称验证集（validation set）。然而在实际应用中，由于数据不容易获取，测试数据极少只使用一次就丢弃。一种改善的方法是$K$折交叉验证（$K$-fold cross-validation）。在$K$折交叉验证中，我们把原始训练数据集分割成$K$个不重合的子数据集，然后我们做$K$次模型训练和验证。每一次，我们使用一个子数据集验证模型，并使用其他$K−1$个子数据集来训练模型。在这$K$次训练和验证中，每次用来验证模型的子数据集都不同。最后，我们对这$K$次训练误差和验证误差分别求平均。

欠拟合和过拟合是什么

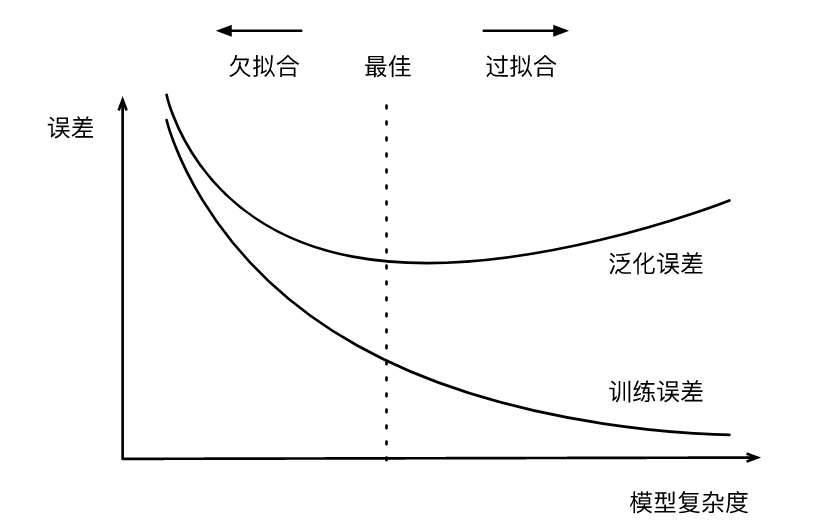
在模型训练中经常出现的两类典型问题：一类是模型无法得到较低的训练误差，我们将这一现象称作欠拟合（underfitting）；另一类是模型的训练误差远小于它在测试数据集上的误差，我们称该现象为过拟合（overfitting）。

虽然有很多因素可能导致这两种拟合问题，在主要两个因素是：模型复杂度和训练数据集大小。

出现过拟合的情况：模型复杂度太高，训练数据集太小
出现欠拟合的情况：模型复杂度太低说一个模型的复杂度高低是和训练数据集的数据特征以及数据规模有关的。如果用一个三阶多项式模型来拟合一个线性模型生成的数据，可以说模型复杂度太高了。在实验中发现，此时虽然网络仍然可以较好拟合出线性模型生成的数据的权重（将高阶权重拟合趋向于0），但此时网络对噪声更加敏感了。当训练数据集规模小于网络模型中的参数时候，这使模型显得过于复杂，以至于容易被训练数据中的噪声影响。而且网络倾向于记住数据的每个特征，这时候容易发生过拟合现象（对训练集的特征学的太好了，泛化能力低），此外，泛化误差不会随训练数据集里样本数量增加而增大。因此，在计算资源允许的范围之内，我们通常希望训练数据集大一些，特别是在模型复杂度较高时，例如层数较多的深度学习模型。相对于欠拟合，我觉得过拟合更容易发生，因为容易设计高复杂度的网络，这时候网络性能瓶颈在于数据规模。下面代码使用多项式拟合实验来测试模型复杂度和训练数据集大小对欠拟合和过拟合的影响，欠拟合是设计一个线性网络拟合一个多项式网络（模型复杂度太低），过拟合是让输入数据规模减小（训练数据集太小）。

代码实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59


from mxnet import autograd, gluon, nd
from mxnet.gluon import data as gdata, loss as gloss ,nn
from matplotlib import pyplot as plt

n_train, n_test, true_w, true_b = 100, 100, [1.2, -3.4, 5.6], 5
features = nd.random.normal(shape=(n_train + n_test, 1))
poly_features = nd.concat(features, nd.power(features, 2),
                          nd.power(features, 3))
labels = (true_w[0] * poly_features[:, 0] + true_w[1] * poly_features[:, 1]
          + true_w[2] * poly_features[:, 2] + true_b)
labels += nd.random.normal(scale=0.1, shape=labels.shape)

def semilogy(x_vals, y_vals, x_label, y_label, x2_vals=None, y2_vals=None,
             title = None,num = None):
    plt.figure(num)
    plt.title(title)
    plt.xlabel((x_label))
    plt.ylabel((y_label))
    plt.plot(x_vals, y_vals)
    if x2_vals and y2_vals:
        plt.plot(x2_vals, y2_vals, linestyle=':')
    plt.pause(0.1)


num_epochs, loss = 100, gloss.L2Loss()

def fit_and_plot(train_features, test_features, train_labels, test_labels,title,num):
    net = nn.Sequential()
    net.add(nn.Dense(1))
    net.initialize()
    batch_size = min(10, train_labels.shape[0])
    train_iter = gdata.DataLoader(gdata.ArrayDataset(
        train_features, train_labels), batch_size, shuffle=True)
    trainer = gluon.Trainer(net.collect_params(), 'sgd',
                            {'learning_rate': 0.01})
    train_ls, test_ls = [], []
    for _ in range(num_epochs):
        for X, y in train_iter:
            with autograd.record():
                l = loss(net(X), y)
            l.backward()
            trainer.step(batch_size)
        train_ls.append(loss(net(train_features),
                             train_labels).mean().asscalar())
        test_ls.append(loss(net(test_features),
                            test_labels).mean().asscalar())
    print('final epoch: train loss', train_ls[-1], 'test loss', test_ls[-1])
    semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
             range(1, num_epochs + 1), test_ls, title,num)
    print('weight:', net[0].weight.data().asnumpy(),
          '\nbias:', net[0].bias.data().asnumpy())

fit_and_plot(poly_features[:n_train, :], poly_features[n_train:, :],labels[:n_train], labels[n_train:],'fit',1)

fit_and_plot(features[:n_train, :], features[n_train:, :], labels[:n_train],labels[n_train:],'underfit',2)

fit_and_plot(poly_features[0:2, :], poly_features[n_train:, :], labels[0:2],labels[n_train:],'overfit',3)

plt.waitforbuttonpress()

实验结果：

拟合
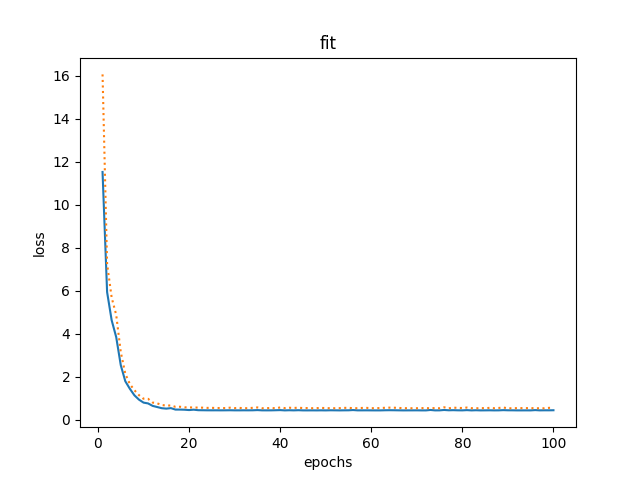
欠拟合
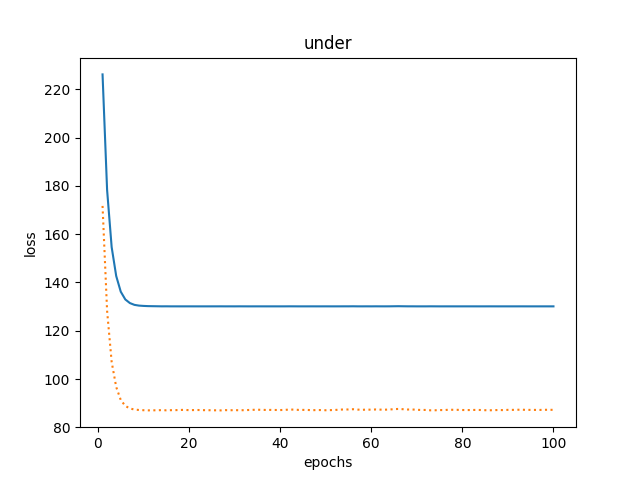
过拟合

模型欠拟合和过拟合

概念

欠拟合和过拟合是什么

代码实现

相关文章：