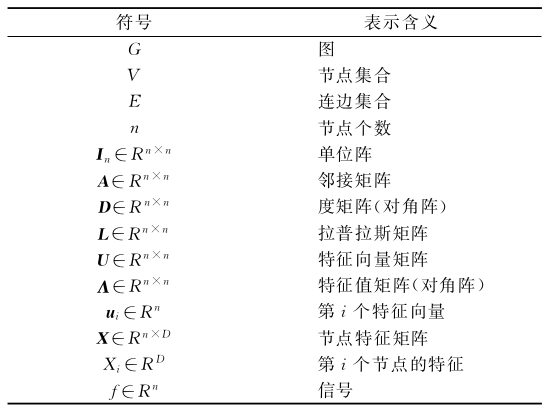
本文中一些重要的符号定义
图卷积神经网络的提出
传统的卷积神经网络只能处理欧氏空间数据 (如图像 、文本和语音 )。以图像数据为例,图像数据规则的栅格形式允许我们在数据空间定义具有全局共享的卷积核,这类型的卷积核和传统的池化操作使得图像数据具有平移不变形。基于此 ,卷积神经网络通过学习在每个像素点共享的卷积核来建模局部连接,进而为图片学习到意义丰富的隐层表示。


但对于非欧数据,传统的卷积操作难以应用到上面。比如图数据和流形数据,这两类数据有个特点就是,排列不整齐,比较的随意。具体体现在:对于数据中的某个点,难以定义出其邻居节点出来,或者是不同节点的邻居节点的数量是不同的,这个其实是一个特别麻烦的问题,因为这样就意味着难以在这类型的数据上定义出和图像等数据上相同的卷积操作出来。
图卷积神经网络关注如何在图上构造深度学习模型,图卷积分为谱域图卷积和空域图卷积,谱域图卷积根据图谱理论和卷积定理,将数据由空域转换到谱域做处理。空域图卷积不依靠图谱卷积理论,直接在空间上定义卷积操作。以这两种卷积算子实现的模型称为谱域图卷积模型与空域图卷积模型。基于卷积定理的图卷积神经网络称为谱域图卷积神经网络,基于设计聚合函数来聚合图上每个中心节点和其邻近节点特征的神经网络称为空域图卷积神经网络。
有关图卷积神经网络的研究,自2019年以来顶会接收的相关文章呈现爆炸性的增长,详情见此github仓库。
谱域图卷积与空域图卷积的联系
谱域图卷积有比较坚实的理论基础,相较于谱域图卷积,空域图卷积的定义直观,灵活性更高。关于他们的联系,这里先直接摆出结论,便于对谱域图卷积的定义形式到空域图卷积的定义形式的演变有一个整体的把握。
- 谱域图卷积的形式表示为:
$$ x_{G}^{*} y=\boldsymbol{U}\left(\left(\boldsymbol{U}^{\mathrm{T}} x\right) \odot\left(\boldsymbol{U}^{\mathrm{T}} y\right)\right) $$
其中$_G^*$表示图卷积算子,$x,y$ 表示图上节点域的信号,$\odot$ 表示哈达玛乘法,则两个向量的对应元素相乘。
- 空域图卷积可以看做特殊形式的一阶切比雪夫卷积:
$$ \mathbf{Y}=\hat{\mathbf{A}} \mathbf{X} \mathbf{W}, \quad \hat{\mathbf{A}} \in R^{N \times N}, \mathbf{X} \in R^{N \times C}, \mathbf{W} \in R^{C \times D} $$
其中 $\hat{\mathbf{A}} =\tilde{\mathbf{D}}^{-1 / 2} \tilde{\mathbf{A}} \tilde{\mathbf{D}}^{-1 / 2}$, $\tilde{\mathbf{A}} = \mathbf{A} + \mathbf{I}$,$\mathbf{A}$指的是邻接矩阵,$\mathbf{I}$指的是单位阵,$ \tilde{\boldsymbol{D}}_{i i}=\sum_{j} \tilde{\boldsymbol{A}}_{i, j} $,$\hat{\mathbf{A}}$是对$\tilde{\mathbf{A}}$的归一化操作,将它的特征值范围约束到0和1之间。
谱域图卷积到空域图卷积的演变过程将在下文陈述。
卷积算子
在信号与处理邻域,由卷积定理,两信号在空域(或者时域)的卷积的傅里叶变换等于这两信号在 谱域(频域)中的傅里叶变换的乘积,即:
$$ \mathcal{F}\left[f_{1}(t) \star f_{2}(t)\right]=F_{1}(w) \cdot F_{2}(w) $$
此公式等价为:
$$ f_{1}(t) \star f_{2}(t)=\mathcal{F}^{-1}\left[F_{1}(w) \cdot F_{2}(w)\right] $$
上面公式可以理解为: 两信号在空域的卷积等价于:先将两信号转到 谱域中进行相乘操作,再将相乘的结果转换到空域。
连续信号的傅里叶变换和反变换:
$$ F(w)=\mathcal{F}[f(t)]=\int_{\mathbb{R}} f(t) e^{-2 \pi i w t} d t $$
$$ f(t)=\mathcal{F}^{-1}[F(w)]=\int_{\mathbb{R}} F(t) e^{2 \pi i w t} d t $$
离散信号的傅里叶变换和反变换:
$$ F(w)=\sum_{t=1}^{n} f(t) e^{-i \frac{2 \pi}{n} w t} $$
$$ f(t)=\frac{1}{n} \sum_{w=1}^{n} F(w) e^{i \frac{2 \pi}{n} w t} $$
不管是连续形式还是离散形式,有空域转为谱域的关键是找到一组正交基,对于$n$维空间,即找到$n$组线性无关的向量。
经典的傅里叶变换有如下规律:傅里叶变换的基函数是拉普拉斯算子的本征函数。严格的数学证明见引用1。拉普拉斯算子定义为梯度的散度:
$$ \Delta f=\nabla \cdot(\nabla f)=\operatorname{div}(\operatorname{grad}(f)) $$
在$n$维欧几里得空间,可以认为拉普拉斯算子是一个二阶微分算子,即在各个维度求二阶导数后求和。
对于离散情况,譬如对于二维图像,两个变量的离散拉普拉斯算子可以写成:
$$ \frac{\partial f}{\partial x}=f^{\prime}(x)=f(x+1)-f(x) $$
$$ \frac{\partial^{2} f}{\partial x^{2}}=f^{\prime \prime}(x)=f^{\prime}(x+1)-f^{\prime}(x)=f(x+1)+f(x-1)-2 f(x) $$
$$ \Delta f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}}=f(x+1, y)+f(x-1, y)+f(x, y-1)+f(x, y+1)-4 f(x, y) $$
将上面公式的每一个正项和负项结合,可以理解为欧氏空间内,二维的拉普拉斯算子是中心节点与周围节点的差值,然后求和。
将该思想拓展到图(graph)上,可以定义图上的拉普拉斯算子:
$$ \Delta f_{i}=\sum_{(i, j) \in \mathcal{E}}\left(f_{i}-f_{j}\right) $$
其中 $\quad f=\left(f_{1}, f_{2}, \cdots f_{n}\right),$ 代表n个节点上每个节点的信号。
谱域图卷积
要定义图上的拉普拉斯算子,有必要先把图的几个基本概念阐述清楚:
基本概念
- 下文中指的图都为无向图
$$ \quad \mathcal{G}=(\mathcal{V}, \mathcal{E}, A) \quad|\mathcal{V}|=n $$
-
邻接矩阵表示顶点与顶点之间的连接关系4 $$ A \in \mathbb{R}^{n \times n} $$
-
度矩阵
$$ \quad D \in \mathbb{R}^{n \times n} \quad D_{i i}=\sum_{j} W_{i j} $$
$D_{ii}$ 表示以顶点 $v_i$为端点的边的数目。
图上定义的拉普拉斯矩阵:
$$ L = D - A $$
上述概念的一个直观的例子:
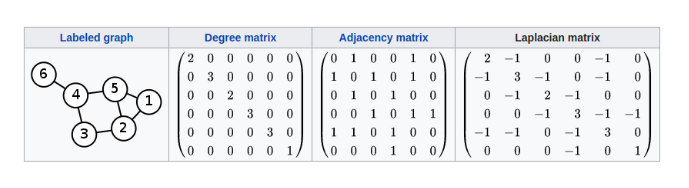
论文2中提出,拉普拉斯矩阵是定义在图上的一种拉普拉斯算子,前面说过傅里叶变换的基函数是拉普拉斯算子的本征函数,类似的,图傅里叶变换的基函数即为拉普拉斯矩阵的特征向量。通过对 $L$的矩阵特征分解,我们可以为图傅里叶变换找到一组正交基。
拉普拉斯矩阵由图的邻接矩阵和度决定,给定一个图,拉普拉斯矩阵是确定的,换句话来说,如果一个图的拓扑形式发生改变,需要重新计算拉普拉斯矩阵。
可以证明,拉普拉斯矩阵$L$是对称半正定矩阵,,对于一个$n$维向量$f$:
$$ f^{T} L f=f^{T} D f-f^{T} W f=\sum_{i=1}^{n} d_{i} f_{i}^{2}-\sum_{i, j=1}^{n} f_{i} f_{j} W_{i j} $$
$$ =\frac{1}{2}\left(\sum_{i=1}^{n} d_{i} f_{i}^{2}-2 \sum_{i, j=1}^{n} f_{i} f_{j} W_{i j}+\sum_{j=1}^{n} d_{j} f_{j}^{2}\right) $$
$$ =\frac{1}{2}\left(\sum_{i, j=1}^{n} W_{i j}\left(f_{i}-f_{j}\right)^{2}\right) \geq 0 $$
作为对称半正定矩阵,拉普拉斯矩阵有如下性质:
-
$n$阶对称矩阵一定有$n$个线性无关的特征向量。
-
对称矩阵的不同特征值对应的特征向量相互正交,这些正交的特征向量构成的矩阵为正交矩阵。
-
实对称矩阵的特征向量一定是实向量
-
半正定矩阵的特征值一定非负。
对拉普拉斯矩阵特征分解:
$$ L=U \Lambda U^{-1} $$
$$ U=\left(\vec{u}_{1}, \vec{u}_{2}, \cdots, \vec{u}_{n}\right) $$
$$ \vec{u}_{i} \in \mathbb{R}^{n}, i=1,2, \cdots n $$
需要说明的是,拉普拉斯矩阵的特征向量组成的矩阵$U$不仅是正交矩阵,它还是标准正交矩阵。这样,通过计算$U=\left(\vec{u}_{1}, \vec{u}_{2}, \cdots, \vec{u}_{n}\right)$,我们可以使用拉普拉斯的特征向量作为基函数,任意的图上的信号可以表示为:
$$ x=\hat{x}\left(\lambda_{1}\right) \vec{u}_{1}+\hat{x}\left(\lambda_{2}\right) \vec{u}_{2}+\cdots+\hat{x}\left(\lambda_{n}\right) \vec{u}_{n} $$
转为矩阵形式,图傅里叶反变换定义如下:

图傅里叶正变换定义如下:
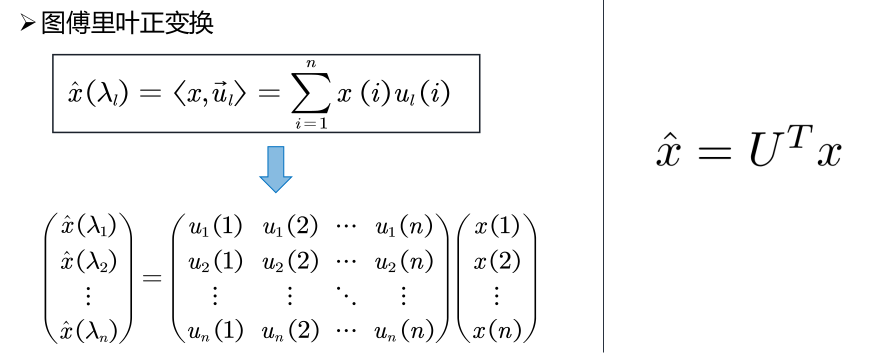
图傅里叶正变换将图上任意信号与每个正交基做内积求出各项的傅里叶系数,图傅里叶反变换是说,图上任意信号可以由一组正交基的线性组合来表示。
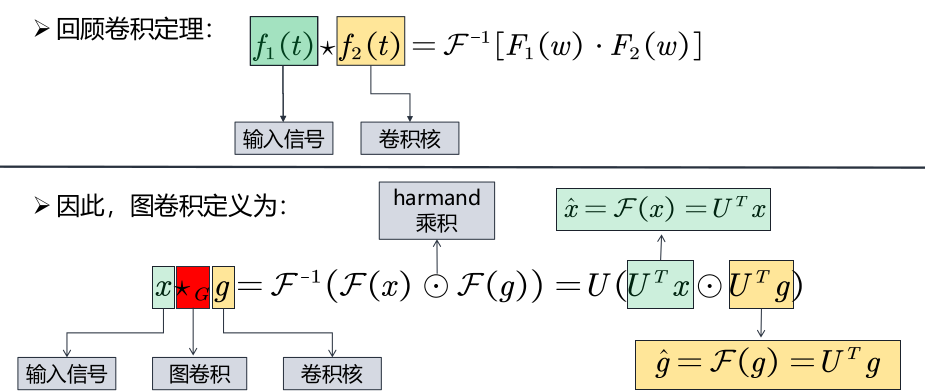
由此得出谱域图卷积的定义:
$$ x_{G}^{*} g=\boldsymbol{U}\left(\left(\boldsymbol{U}^{\mathrm{T}} x\right) \odot\left(\boldsymbol{U}^{\mathrm{T}} g\right)\right) $$
定义 $g_{\theta} = diag(\boldsymbol{U}^Tg) $为谱域上的卷积算子,上述公式还可以表示为:
$$ x ^\star_{G} g_{\theta}=\boldsymbol{U}g_{\theta}\boldsymbol{U}^{\mathrm{T}} x $$
$g_{\theta}$是一个$n$维的对角阵。
有不少关于谱域卷积的工作,SCNN 用可学习的对角矩阵来代替谱域的卷积核;ChebNet 采用切比雪夫多项式来代替谱域的卷积核;GCN 仅考虑1阶切比雪夫多项式,且每个卷积核仅只有一个参数。
谱域图卷积的不足之处
上面的公式在图数据的应用上存在一定的局限性:
- 参与卷积的图上信号$x$是全图的所有节点的信号($x \in \mathbb{R}^{n \times c}$),它不是一个局部链接的结构。
- 由于矩阵$U$是由拉普拉斯矩阵$L$特征分解而来,$L$是一个对称半正定矩阵,这要求处理的图解钩是无向图。
- 由于进行谱域图卷积需要事先确定$L$,在模型训练过程中,图结构不能变化,而在某些场景下,图结构是可能发生变化的(社交网络数据,交通数据等。
空域图卷积
空域图卷积的定义
前面提到,在
$$ x ^\star_{G} g_{\theta}=\boldsymbol{U}g_{\theta}\boldsymbol{U}^{\mathrm{T}} x $$
中,$g_{\theta}$是一个$n$维的对角阵。一个谱域图卷积网络 ChebyNet3对$g_{\theta}$参数化:
$$ \boldsymbol{g}_{\theta}=\sum_{i=0}^{K-1} \theta_{k} T_{k}(\hat{\Lambda}) $$ 其中 $ \theta_{k}$ 是需要学的系数 ,$\hat{\Lambda}=\frac{2 \Lambda}{\lambda_{\max }}-\mathbf{I}_{n} $。 切比雪夫多项式是通过递归得到,递归表达式为
$$ T_{k}(x)=2 x T_{k-1}(x)-T_{k-2}(x) $$
其中,
$$ T_{0}(x)=1, T_{1}(x)=x $$
这样,有:
$$ x ^\star_{G} g_{\theta} =U g_{\theta} U^{T} x =U \sum_{k=0}^{K} \beta_{k} T_{k}(\hat{\Lambda}) U^{T}x $$
$$ = \sum_{k=0}^{K} \beta_{k} T_{k}(U \hat{\Lambda} U^{T}) x =\sum_{k=0}^{K} \beta_{k} T_{k}(\hat{L}) x $$
其中$\hat{L}=\frac{2}{\lambda_{\max }}\tilde L-I_{n}$, $\lambda_{\max } = 2$,$\tilde L$表示归一化的拉普拉斯矩阵: $\tilde L = I_n - D^{-1/2}AD^{-1/2}$,故$\hat{L}$的表达式最终化简为:
$$ \hat{L} = - D^{-1/2}AD^{-1/2} $$
当仅考虑一阶切比雪夫多项式,即$K = 1$时,
$$ x \star_{G} g_{\theta} =\sum_{k=0}^{K} \beta_{k} T_{k}(\hat{L}) x=\sum_{k=0}^{1} \beta_{k} T_{k}(\hat{L}) x $$
$$ =\beta_{0} T_{0}(\hat{L}) x+\beta_{1} T_{1}(\hat{L}) x =\left(\beta_{0}+\beta_{1} \hat{L}\right) x $$
令 $\beta_{1} = -\beta_{0}$,
故:
$$ x \star_{G} g_{\theta} = \left(\beta_{0}+\beta_{1} \hat{L}\right) x = \beta_{0}\left( I_n + D^{-1/2}AD^{-1/2}\right)x $$
由于$I_n + D^{-1/2}AD^{-1/2}$具有[0,2]的特征值,如果在深度神经网络模型中使 用该算子,则反复应用该算子会导致数值不稳定(发散)和梯度爆炸/消失, 为了解决该问题, 引入了一个 renormalization trick:
$$ I_{n}+D^{-1 / 2} A D^{-1 / 2} \rightarrow \tilde{D}^{-1 / 2} \tilde{A} \tilde{D}^{-1 / 2} $$
$$ \tilde{A}=A+I_{n} \quad \tilde{D}_{i i}=\sum \tilde{A}_{i j} $$
这其实是谱域GCN(图卷积网络)参数化的卷积函数,但从空域的角度来看,一阶图卷积网络将$\tilde{D}^{-1 / 2} \tilde{A} \tilde{D}^{-1 / 2}$当做聚合函数,令$\hat{\mathbf{A}} =\tilde{\mathbf{D}}^{-1 / 2} \tilde{\mathbf{A}} \tilde{\mathbf{D}}^{-1 / 2}$,有:
$$ x \star_{G} g_{\theta} = \beta_{0}\hat{\mathbf{A}}x $$
从空域的理解上面的式子,它的物理意义是:
- 为图上节点添加自连接边
- 局部空间信息融合
- 归一化
这里的 $\beta_{0}$是一个尺度因子,在神经网络模型中会被归一化操作替代,因此不妨设$\beta_{0} = 1$,为了加强网络的拟合能力,有研究引入一个参数化的权重矩阵$W$对输入的图信号矩阵$x$做仿射变换,于是有:
$$ \mathbf{Y} = x \star_{G} g_{\theta} = \hat{\mathbf{A}}x \mathbf{W} $$
$$ \hat{\mathbf{A}} \in R^{N \times N}, x \in R^{N \times C}, \mathbf{W} \in R^{C \times D} $$
为和文章开始引入的公式对齐,令 $x = \mathbf{X}$,故单层的空域上的图卷积层可以定义为:
$$ \mathbf X' = \sigma \left(\hat{\mathbf{A}}\mathbf{X} \mathbf{W}\right) $$
可以看到空间域图卷积实际上可以由一阶切比雪夫卷积导出,它也可以看做GCN在空域视角的表达形式。
空域图卷积的几个模型介绍
作为深度学习域图数据结合的代表性方法,GCN的出现带动了将神经网络技术运用到图数据的学习任务中去的一大类方法。从空域角度看GCN,本质上是一个迭代式地聚合邻居的过程,这启发了一大类模型对于这种聚类操作的重新设计,以加强模型对于图数据的适应性,下面将介绍几个空域图卷积的模型。
- GAT
GAT4即 GRAPH ATTENTION NETWORKS,其核心思想为将attention引入到图卷积模型中。图注意力网络利用注意力机制定义聚合函数,与以往关心边上信息的模型不同,在图注意力网络中,邻接矩阵仅被用来定义相关节点,而关联权重的计算则是依赖于节点的特征表达。图注意力网络的每一层结构如下图所示:
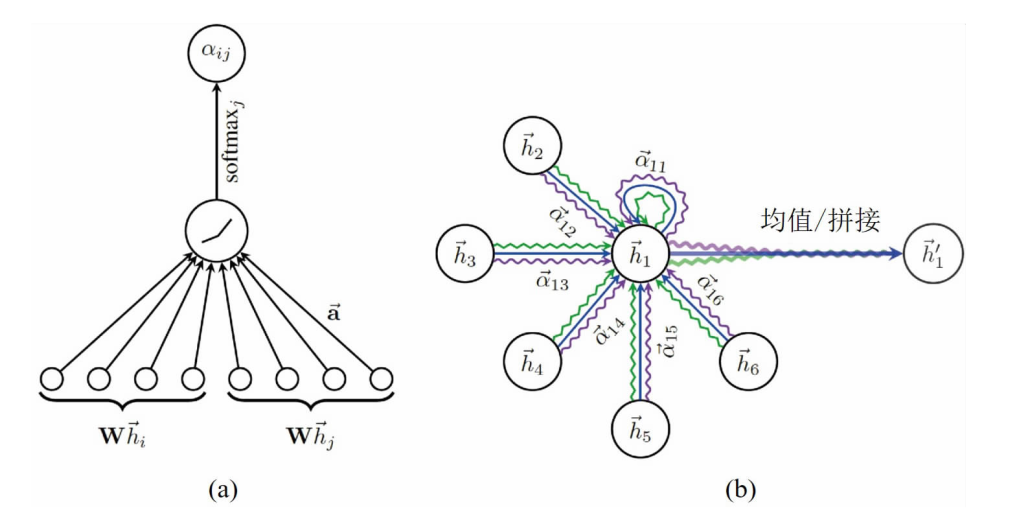
1.使用注意力机制计算节点之间的关联度
$$ e_{i j}=\alpha\left(\mathbf{W} \vec{h}_{i}, \mathbf{W} \vec{h}_{j}\right)=\vec{a}^{T}\left[\mathbf{W} \vec{h}_{i}|| \mathbf{W} \vec{h}_{j}\right] $$
其中 $\vec{h}_{i} \in \mathbb{R}^{F}$ 表示i节点的特征, F表示节点特征 的通道数。$W \in \mathbb{R}^{F \times F^{\prime}}$ 是可学习的线性变换参数。 $\alpha(\cdot): \mathbb{R}^{F^{\prime}} \times \mathbb{R}^{F^{\prime}} \rightarrow \mathbb{R}$ 表示注意力机制, 其输出 $e_{i j}$ 为注意力系数。 在实验中 $\alpha(\cdot)$ 的实现是一个单层前馈神经网络。 ||表示拼接。 $\vec{a}^{T} \in \mathbb{R}^{2 F^{\prime}}$ 为可学习参数。
用softmax 归一化注意力系数:
$$
\alpha_{i j}=\operatorname{softmax}_{j}\left(e_{i j}\right)=\frac{\exp \left(e_{i j}\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(e_{i k}\right)}
$$
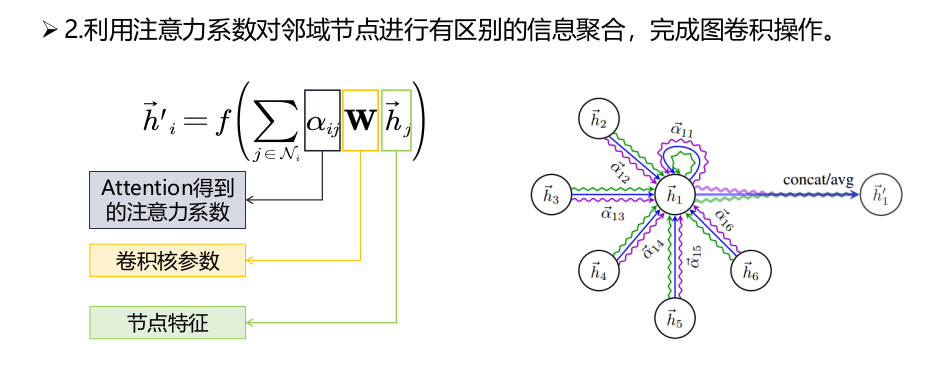
若将$\alpha_{i j}$和$\mathbf{W} $结合起来看做一个系数,实际上GAT对邻域的每个节点隐式地(implicitly)分配了不同的卷积核参数。
从图注意力网络开始 ,节点之间的权重计算开始从依赖于网络的结构信息转移到依赖于节点的 特征表达 ,但是以上模型在处理时需要加载整个网络的节点特征 ,这阻碍了模型在大规模网络上的应用。
- GraphSAGE
GraphSAGE5不同于以往模型考虑所有邻近节点 ,图采样聚合网络对邻近节点做随机采样 ,使得每个节点的邻近节点都小于给定的采样个数.
GraphSAGE认为卷积可以理解为采样和信息聚合两个步骤的结合,邻域的节点不需要进行排序,设计的聚合函数需要与输入顺序无关。
GraphSAGE 的聚合函数有多种形式,分别是基于最大值的聚合,基于均值的聚合和长短时记忆力网络(LSTM)。最大值聚合和均值聚合分别指取相关节点的最大值和均值作为聚合结果。长短时记忆网络指将相关节点输入LSTM,并把输出作为聚合结果。
 图采样聚合网络提出用分批量处理数据的方法训练模型 ,在每个批量输入数据下只需要加载对应节点的局部结构 ,避免了整张网络的加载,这使得在大规模数据集上搭建图卷积神经网络成为可能。
图采样聚合网络提出用分批量处理数据的方法训练模型 ,在每个批量输入数据下只需要加载对应节点的局部结构 ,避免了整张网络的加载,这使得在大规模数据集上搭建图卷积神经网络成为可能。
- PGC
PGC6将卷积理解为特定的采样函数与特定的权重函数相乘后求和。与GraphSAGE认为邻域不需要排序,并且使用均值采样确定邻域不同,PGC采用更加泛化的方式,为邻域节点根据某种度量分类,不同的类别分配不同的权重函数。
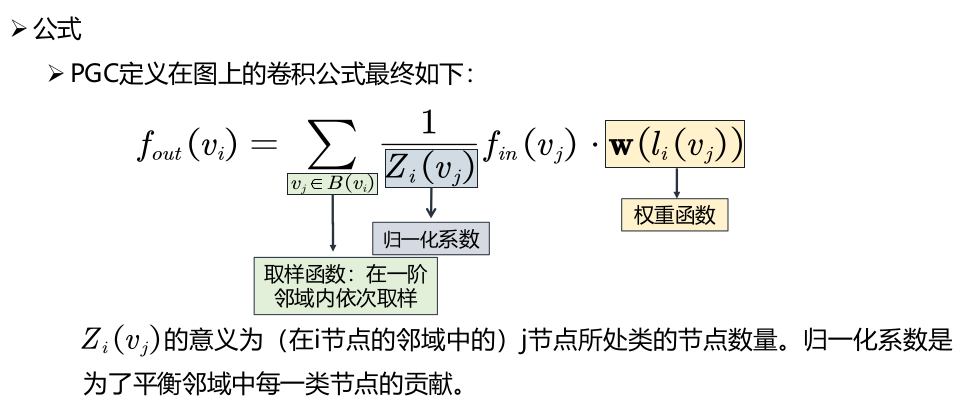
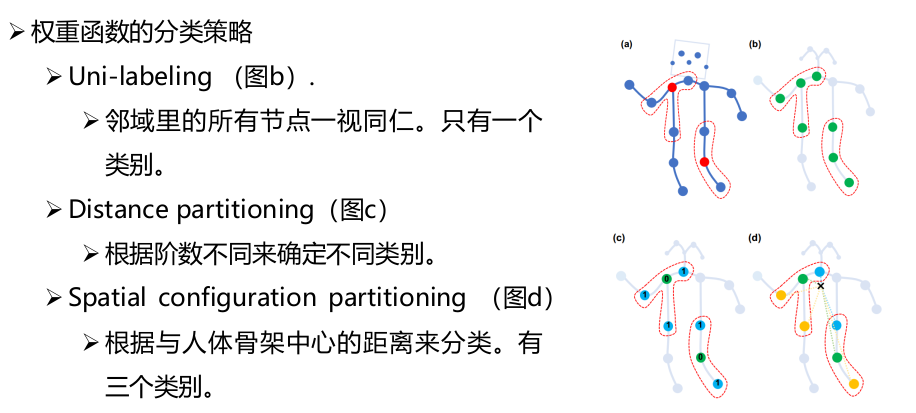
池化算子
在传统的卷积神经网络中,卷积会和池化相结合 ,池化算子一方面能够减少学习的参数 ,另外一方面能反应输入数据的层次结构 ,而在图卷积神经网络中 ,在解决节点级别的任务如节点分类,链接预测时,池化算子并非必要。但在图层面的学习任务中,如图分类问题需要关注图数据的全局信息,既包含图的结构信息,也包含各个节点的属性信息,模型的重点在于如何学习一个优秀的全图表示向量,在这个层面上,如何实现层次化池化机制是GNN需要解决的基础问题。
层次化池化机制的几种实现思路
- 基于图坍塌的池化机制
图坍塌是将图划分为不同的子图,然后将子图视为超级节点,从而形成一个坍塌的图。
- 基于TopK 的池化机制
对图中每个节点学习出一个分数,基于这个分数的排序丢弃一些低分数的节点,这类方法借鉴了CNN中最大池化操作的思路:将更重要的信息筛选出来。所不同的是,图数据难以实现局部滑窗操作,因此需要依据分数进行全局筛选。
- 基于边收缩的池化操作
边收缩是指并行地将图中的边移除,并将移除边的两个节点合并,同时保持被移除节点的连接关系,该思路通过归并操作来逐步学习图的全局信息的方法。
图卷积神经网络的过平滑现象以及缓解方案
GCN的过平滑现象
论文7在图卷积神经网络的协同训练展开详细分析 ,指出 GCN 的本质是拉普拉斯平滑。
对图做拉普拉斯平滑,其形式如下: $$ \left(\boldsymbol{I}-\gamma \hat{\boldsymbol{D}}^{-1} \hat{\boldsymbol{L}}\right) X $$ 其中 $, \hat{L}=\hat{D}-\hat{A}, 0<\gamma<1$ 是超参数,用以调节源节点 和周围节点的权重.令 $\gamma=1$,则拉普拉斯平滑形式为 $\hat{\mathbf{D}}^{-1} \hat{\boldsymbol{A}} X,$ 此时如果用对称标准化的拉普拉斯算子 $\hat{\boldsymbol{D}}^{-\frac{1}{2}} \hat{\boldsymbol{L}} \hat{\boldsymbol{D}}^{-\frac{1}{2}}$ 替代 $\hat{\boldsymbol{D}}^{-1} \hat{\boldsymbol{L}},$ 则上式等价为 $\hat{\boldsymbol{D}}^{-\frac{1}{2}} \hat{\boldsymbol{A}} \hat{\boldsymbol{D}}^{-\frac{1}{2}} X$ 由此可见,GCN 的本质是在网络上做拉普拉斯平 滑.拉普拉斯平滑使用每个节点的邻居及自身表达 的加权和作为当前节点的新特征,由于在分类任务 中,同类节点倾向于稠密连接,平滑使得同类节点的 特征更为相似,进而提升了下游的分类任务.同时文 章指出,多层的 GCN 在更新目标节点表达时,会混合其他类节点的信息,进而导致效果降低,这是多层GCN存在的过平滑现象。
过平滑现象的缓解方案
浅层图卷积网络的感受野,特征提取能力有限,多层图卷积网络具有强大特征提取能力,但多次拉普拉斯平滑会使输出特征过度平滑,同时会带来梯度消失,过拟合的问题。
缓解过平滑问题的一些方法:
- 深度拓展:高层特征融合底层特征
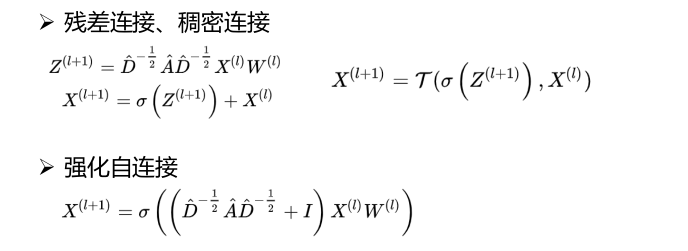
- 宽度拓展:全局特征融合局部特征

图卷积神经网络的任务分类
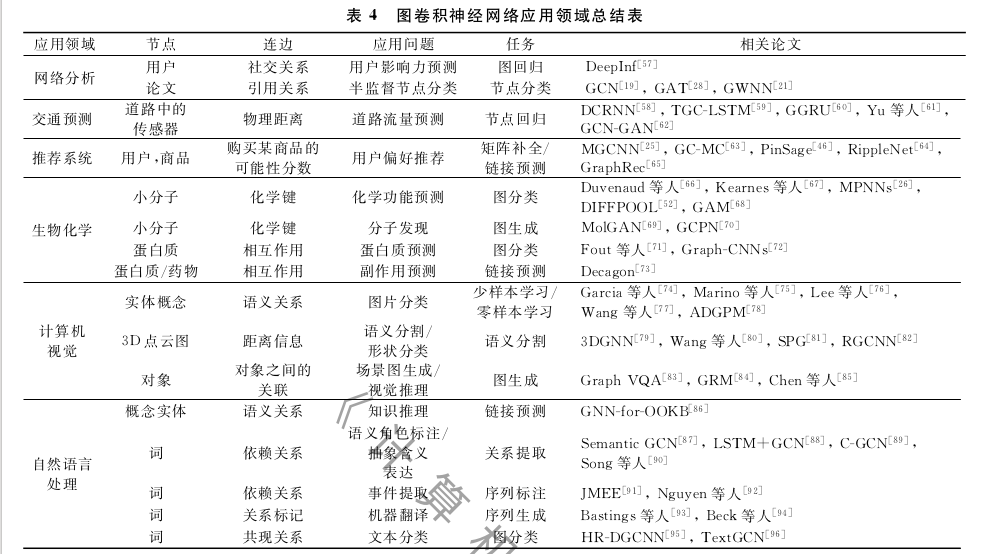
图卷积神经网络在计算机视觉中的应用
- 基于图匹配的直线匹配
- 基于谱聚类的模型拟合
参考文献
- [1] The Emerging Field of Signal Processing on Graphs: Extending High-Dimensional Data Analysis to Networks and other Irregular Domains. IEEE Signal Processing Magazine
- [2] Discrete Regularization on Weighted Graphs for Image and Mesh Filtering
- [3] Convolutional neural networks on graphs with fast localized spectral filtering. In Advances in neural information processing systems (NIPS), 2016.
- [4] Graph Attention Networks ICLR 2018
- [5] Inductive representation learning on large graphs, in Proc. of NIPS, 2017
- [6] Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action. AAAI. 2018.
- [7] Deeper Insights into Graph Convolutional Networks for Semi-Supervised Learning, in AAAI 2019.