图的概念回顾
对于一个图$G$，我们一般用点的集合$V$和边的集合$E$来描述。即为$G(V,E)$。其中$V$即为我们数据集里面所有的点$(v1,v2,...vn)$。对于$V$中的任意两个点，可以有边连接，也可以没有边连接。我们定义权重$w_{ij}$为点 $v_i$ 和点 $v_j$ 之间的权重。
对于有边连接的两个点$v_i$和$v_j$，$w_{ij}>0$,对于没有边连接的两个点$v_i$和$v_j$，$w_{ij}=0$。对于图中的任意一个点$v_i$，它的度$d_i$定义为和它相连的所有边的权重之和，即
$$ d_i = \sum\limits_{j=1}^{n}w_{ij} $$
利用每个点度的定义，我们可以得到一个$n \times n$的度矩阵$D$,它是一个对角矩阵，只有主对角线有值，对应第$i$行的第$i$个点的度数$d_i $
minCT 和 谱聚类
谱聚类是从图论中演化出来的算法，后来在聚类中得到了广泛的应用。它的主要思想是把所有的数据看做空间中的点，这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高，通过对所有数据点组成的图进行切图，让切图后不同的子图间边权重和尽可能的低，而子图内的边权重和尽可能的高，从而达到聚类的目的。
给定一个图$G(V,E)$，K向归一化 minCUT 问题（简称为 minCUT ）通过去除最小权重边将$V$划分为$K$个不相交子集 。 问题等同于最大化：
$$ \frac{1}{K} \sum_{k=1}^{K} \frac{\operatorname{links}\left(\mathcal{V}_{k}\right)}{\operatorname{degree}\left(\mathcal{V}_{k}\right)}=\frac{1}{K} \sum_{k=1}^{K} \frac{\sum_{i, j \in \mathcal{V}_{k}} \mathcal{E}_{i, j}}{\sum_{i \in \mathcal{V}_{k}, j \in \mathcal{V} \backslash \mathcal{V}_{k}} \mathcal{E}_{i, j}} $$
其中分子计算一个划分内节点的边权重之和，分母计算一个划分内的节点和其划分的补集内节点的连接边的权重之和。
让 $\mathbf{C} \in{0,1}^{N \times K}$ 为聚类分配矩阵, $\mathbf{C}_{i, j}=1$代表 $i$ 属于划分 $j,$ 否则为0. minCUT 问题可以表示为:
$$ \text { maximize } \frac{1}{K} \sum_{k=1}^{K} \frac{\mathbf{C}_{k}^{T} \mathbf{A} \mathbf{C}_{k}}{\mathbf{C}_{k}^{T} \mathbf{D} \mathbf{C}_{k}} $$
$$ \text { s.t. } \mathbf{C} \in{0,1}^{N \times K}, \mathbf{C 1}_{K}=\mathbf{1}_{N} $$
其中 $\mathbf{C}_{k}$ 代表 $\mathbf{C}$的第$k$ 列. 该问题是个 NP-hard 的问题, 但它可以松弛到另外一个可以用多项式时间内解决的问题，并保证了接近最佳的解决方案： $$ \underset{\mathbf{Q} \in \mathbb{R}^{{N} \times K}}{\arg \max } \frac{1}{K} \sum_{k=1}^{K} \mathbf{Q}_{k}^{T} \mathbf{A} \mathbf{Q}_{k} $$
$$ \text { s.t. } \mathbf{Q}=\mathbf{C}\left(\mathbf{C}^{T} \mathbf{D} \mathbf{C}\right)^{-\frac{1}{2}}, \mathbf{Q}^{T} \mathbf{Q}=\mathbf{I} _{K} $$ 虽然上述的问题仍然是非凸的, 它有一个最优的解： $\mathbf{Q}^{*}=\mathbf{U}_{K} \mathbf{O},$ 其中 $\mathbf{U}_{K} \in \mathbb{R}^{N \times K}$ 是矩阵 $\mathbf{A}$ 的前 $K$ 个最大特征向量组成的矩阵。$\mathbf{O} \in \mathbb{R}^{{K} \times {K}}$是正交变换矩阵。
在此之后对$\mathbf{Q}^{*}$做一个 k-mean 聚类，至此完成谱聚类的全部流程。
利用GNN做谱聚类
网络结构
基于这样的假设：同一划分中的节点之间是强连接的，同一划分中的节点间的特征是相似的，利用GNN的消息传播机制，节点的邻域特征得到聚合，强连接的节点的特征趋向于更加相似。在论文1中，聚类分配矩阵用一个多层感知机表示，具体如下：
让 $\mathbf{X}$ 代表节点特征矩阵. 文章让$\mathbf{X}$通过一个或多个消息传播层( MP )得到$\overline{\mathbf{X}}$，再通过 MLP 层计算聚类分配矩阵 $\mathbf{S}$，并且在输出层加上 softmax 层对输出数据归一化:
$$ \overline{\mathbf{X}} =\operatorname{GNN}\left(\mathbf{X}, \tilde{\mathbf{A}} ; \Theta_{\mathrm{GNN}}\right) $$
$$ \mathbf{S} =\operatorname{MLP}\left(\overline{\mathbf{X}} ; \Theta_{\mathrm{MLP}}\right) $$ 其中 $\Theta_{\text {GNN }}$ and $\Theta_{\text {MLP }}$ 是可训练参数. softmax 层保证了$s_{i j} \in[0,1]$ 并且满足了约束：$\mathbf{S} \mathbf{1}_{K}=\mathbf{1}_{N}$.
损失函数
网络参数 $\Theta_{\text {GNN }}$ 和 $\Theta_{\text {MLP }}$ 通过无监督损失函数$\mathcal{L}_{u}$被联合优化:
$$ \mathcal{L}_{u}=\mathcal{L}_{c}+\mathcal{L}_{o}=\underbrace{-\frac{\operatorname{Tr}\left(\mathbf{S}^{T} \tilde{\mathbf{A}} \mathbf{S}\right)}{\operatorname{Tr}\left(\mathbf{S}^{T} \tilde{\mathbf{D}} \mathbf{S}\right)}}_{\mathcal{L}_{c}}+\underbrace{\left|\frac{\mathbf{S}^{T} \mathbf{S}}{\left|\mathbf{S}^{T} \mathbf{S}\right|_{F}}-\frac{\mathbf{I}_{K}}{\sqrt{K}}\right|_{F}}_{\mathcal{L}_{o}} $$ 其中 $|\cdot|_{F}$ 表示 Frobenius 范数.$\mathcal{L}_{c}$形式类似于上面的 minCUT 求最优解的问题，$\mathcal{L}_{o}$是一个正则项，它让学习出来的$\mathbf{S}$趋向于正交矩阵以及聚类后每一个划分的节点数趋向相似的大小。
建图
构建特征矩阵$X$
由于上图的任务是从数据中提取直线，数据中每两个点构成一个直线模型假设，设图中离散点的数目为$N$，生成的总假设模型数为$M$，即在原始数据中随机采样$M$次生成所有的假设模型，然后对于数据中每个离散点，考察该点到$M$个假设模型的距离。这样可以构建一个维度为$N \times M$的特征矩阵$X$，当第$i$点到假设模型$j$的欧氏距离小于等于给定阈值$T$，$X_(i,j)=1$,否则$X_(i,j)=0$。
构建邻接矩阵$A$
构建一个合理的邻接矩阵有助于网络收敛，代码中为每个节点选择K个邻域节点，具体方式如下：
在步骤1中，每个节点表示为一个$M$维向量，为给每个节点寻找$K$近邻，需要在$N$个$M$维向量中为每个向量寻找相似度最高的$K$个向量，代码中用 faiss 库完成向量相似度检索。
这样我们就得到了一个N×N维的稀疏矩阵A。
数据转换保存
保存特征矩阵X，邻接矩阵A以及原始数据坐标，并转换为pytorch geometric需要的数据格式，完成建图。
网络结构选取
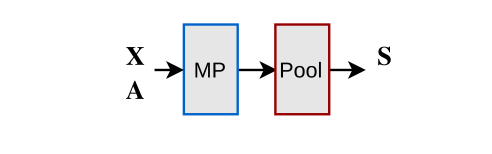消息传播层( MP )可以是一层或多层 GNN 层的堆叠，在试验中我选用了 GENeralized Aggregation Networks (GEN)2 ,它是 GCN 的一个变体，相较 GCN 文章首先提出可微的广义消息聚合
函数，它定义了一系列置换不变函数，并且进一步介绍了残余连接和消息规范化层的新变体，这有助于节点特征的更有效聚合。
池化层( Pool )采用的是文章1提出的 MinCutPool 层。
实验结果
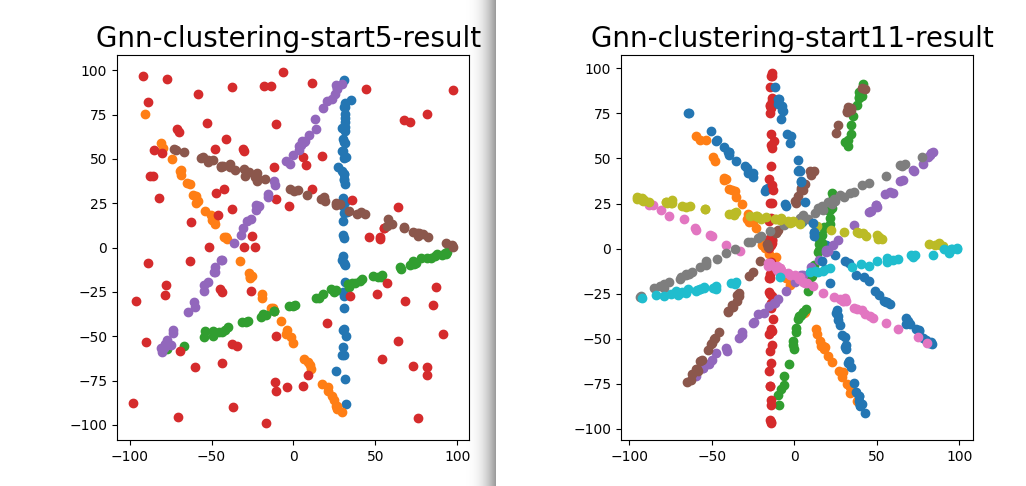
直线聚类结果
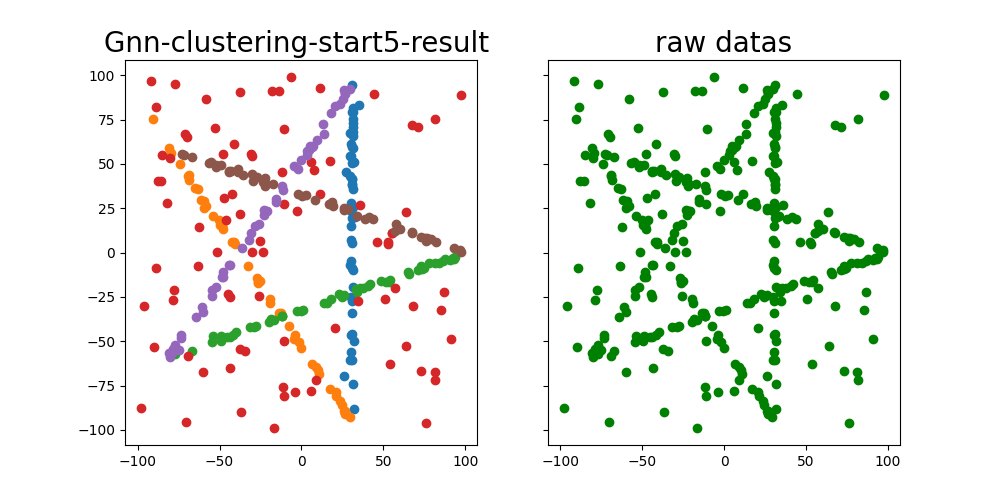
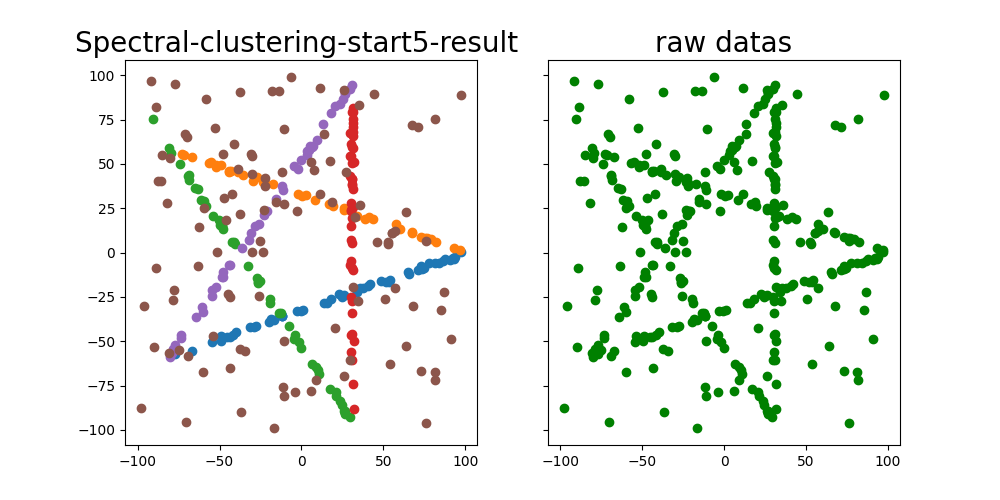
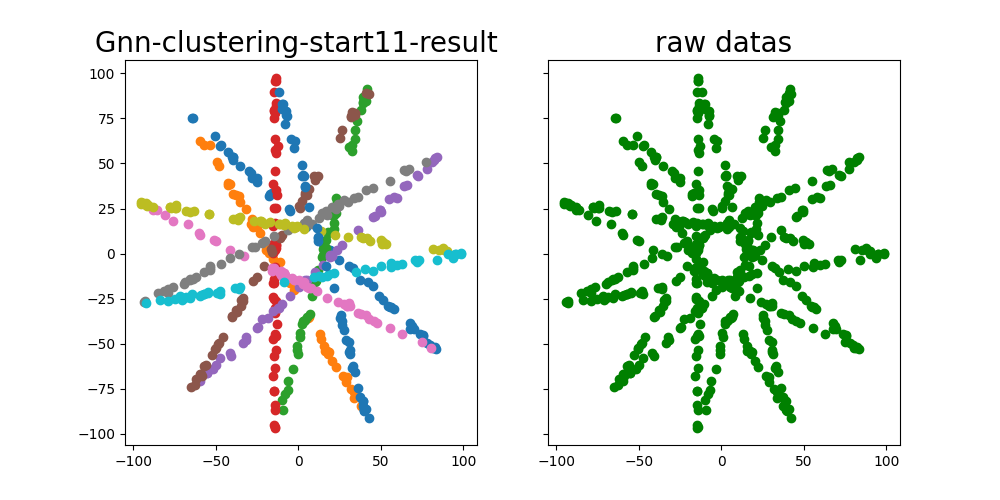
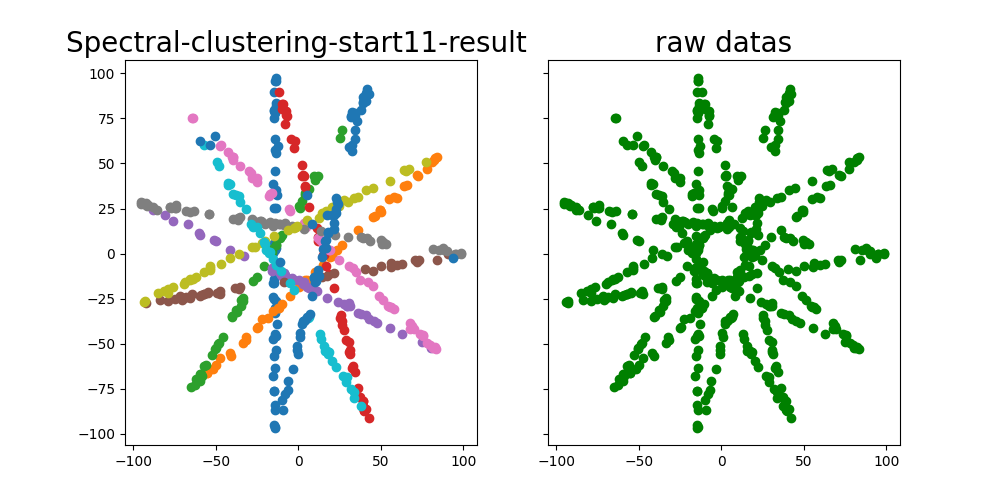
二次曲线聚类结果
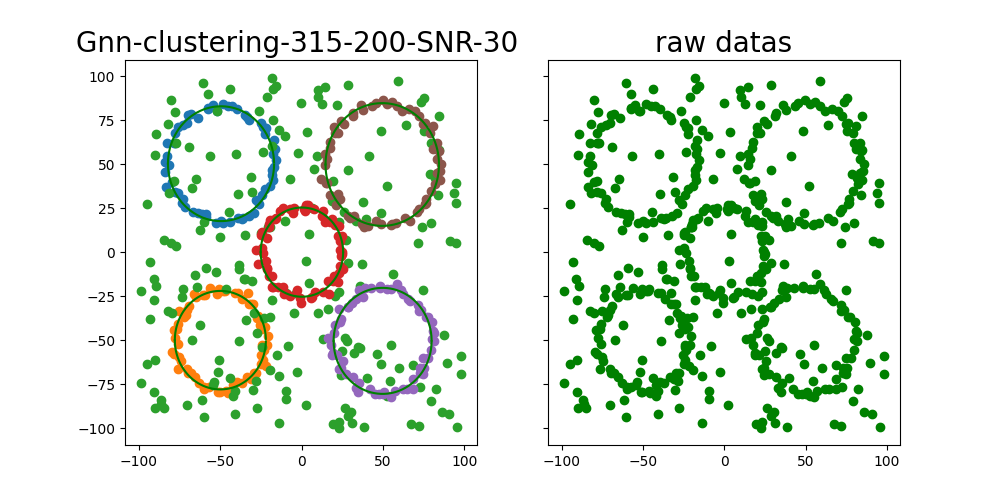
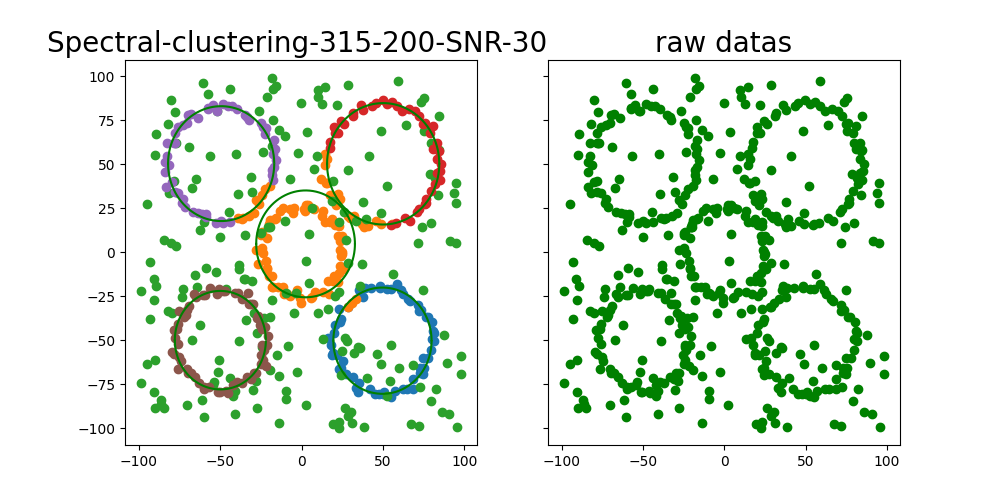
目前发现该方法不足之处
-
聚类的划分数需要事先确定，若数据中存在待拟合的模型数未知，网络难以收敛，或者收敛到一个不理想的结果。
-
聚类结果好坏依赖于构建的初始邻接矩阵的质量，虽然在试验中发现一些 GNN 层能有效地动态改变图中节点的邻接关系，但对于模型数较多的数据(如 star11 )，当初始邻接矩阵不理想，拟合效果仍然不好。
参考文献
-[1] Spectral Clustering with Graph Neural Networks for Graph Pooling
-[2] DeeperGCN: All You Need to Train Deeper GCNs