本文记录两视图的对极几何的概念和基本矩阵的概念，以及给定第一幅视图的像点$\mathbf{x}$，它怎么约束第二幅视 图的对应点$\mathbf{x}^{\prime}$的位置的问题。
概念
对极几何是两幅视图之间内在的射影几何，它独立于景物结构，只依赖于摄像机的内参数和相对姿态。对极几何可以由3×3矩阵$F$表示，称为基本矩阵，它是一个秩为2的矩阵，如果一个三维空间点$\mathbf{X}$在第一，第二幅视图中的像点为$\mathbf{x}$，$\mathbf{x}^{\prime}$，则这两个图像点满足关系$\mathbf{x}^{\prime T}F\mathbf{x}=0$
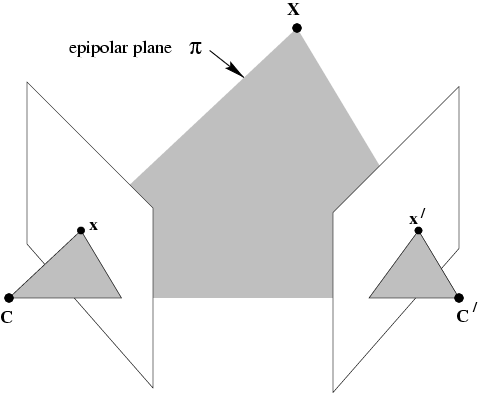两幅视图之间的对极几何是图像平面与以基线（连接两摄像机中心的直线）为轴的平面束（极平面束）的交的几何。如上图，确定了两相机的光心$\mathbf{c},\mathbf{c}^{\prime}$和像点$\mathbf{x}$，由于空间点$\mathbf{X}$在过$\mathbf{c},\mathbf{x}$的射线上，该射线被投影到第二幅视图中被影像成一条直线（极线）$\mathbf{I}^{\prime}$，空间点$\mathbf{X}$对应的第二幅视图像点$\mathbf{x}^{\prime}$（极点）就落在直线$\mathbf{I}^{\prime}$上。用公式表示为：
$$
\mathbf{I}^{\prime}=F \mathbf{x}
$$
$F$为基本矩阵。
基本矩阵$F$的代数形式
F 表征着$\mathbf{I}^{\prime}$与$\mathbf{x}$的关系。在摄像机矩阵$P$作用下，从$\mathbf{x}$反向投影的射线通过解方程$P\mathbf{X}=\mathbf{x}$得到，其解的形式为： $$ \mathbf{X}(\lambda)=P^{+} \mathbf{x}+\lambda \mathbf{C} $$ 其中$P^{+}$是$P$的伪逆，则$P P^{+}=I$，该射线上有两个特殊的点$P^{+} \mathbf{x}$和$\mathbf{C}$分别被映射到第二幅视图上的点$P^{\prime} P^{+} \mathbf{x}$和$P^{\prime} \mathbf{C}$上($P^{\prime} $是第二幅视图的摄像机矩阵)，故$\mathbf{I}^{\prime}$可以表示为： $$ \mathbf{I}^{\prime}=\left(P^{\prime} \mathbf{C}\right) \times\left(P^{\prime} P^{+} \mathbf{x}\right)=F\mathbf{x} $$ 由于 $$ \mathrm{e}^{\prime} = \left(P^{\prime} \mathbf{C}\right) $$ 故
$$ F=\left[\mathrm{e}^{\prime}\right]_{ \times} P^{\prime} P^{+} $$
其中$\left[\mathrm{e}^{\prime}\right]_{ \times}$表示$\mathrm{e}^{\prime}$的反对称矩阵。
由$F$恢复摄像机矩阵
上面的$F$可以由摄像机矩阵$P$和$P^{\prime} $唯一确定，但反过来并不成立。给定$F$仅能在射影变换意义下恢复摄像机矩阵。
如果$H$是一个3维射影变换的一个4×4的矩阵，那么对应于摄像机矩阵$(P,P^{\prime})$和$(PH,P^{\prime}H)$的基本矩阵是相同的。
摄像机矩阵的规范形式
对应于摄像机矩阵，对$P=[I | 0]$和$P^{\prime}=[M | \mathrm{m}]$的基本矩阵是$[\mathbf{m}]_{ \times} M$
给定$F$后摄像机射影多义性
令$F$为基本矩阵而$\left(P, P^{\prime}\right)$和$\left(\tilde{P}, \tilde{P}^{\prime}\right)$都是于基本矩阵$F$对应的两组摄像机矩阵对，则存在一个非奇异矩阵$H$，使得$\widehat{\mathrm{P}}=\mathrm{PH}$和$\tilde{P}^{\prime}=P^{\prime} H$。令$P=\widetilde{P}=[\mathrm{I} | \mathbf{0}]$，$P^{\prime}=[A | \mathbf{a}]$，$\tilde{P}^{\prime}=[\tilde{A} | \tilde{\mathbf{a}}]$，此时$F$可以分解为两种不同的形式：
$$ F=[\mathrm{a}]_{ \times}A $$
$$ F=[\tilde{\mathrm{a}}]_{\times} \tilde{A} $$
这两种形式的对应关系为：$\widetilde{\mathbf{a}}=k \mathbf{a}$和$\tilde{A}=k^{-1}\left(A+\mathbf{a}\mathbf{v}^{T}\right)$，其中$k$为非零常数，$\mathbf{v}$是三维矢量。
给定$F$求规范摄像机对
可以选择为两种形式：
$\mathrm{P}=[I| \mathbf{0}]$ 和 $P^{\prime}=\left[\left[\mathrm{e}^{\prime}\right]_{ \times} F | \mathrm{e}^{\prime}\right]$
$\mathrm{P}=[I | \mathbf{0}]$和 $P^{\prime}=\left[\left[\mathrm{e}^{\prime}\right]_{ \times} F+\mathrm{e}^{\prime} \mathbf{v}^{\mathrm{T}} | \lambda \mathrm{e}^{\prime}\right]$
公式的推导我直接放图了：
