用光流跟踪特征点和用直接法计算相机位姿。
尽管特征点法在视觉里程计中占据主流地位,研究者们认识到它至少有以下几个缺点:
-
关键点的提取与描述子的计算非常耗时。实践当中,SIFT 目前在 CPU 上是无法实
时计算的,而 ORB 也需要近 20 毫秒的计算。如果整个 SLAM 以 30 毫秒/帧的速
度运行,那么一大半时间都花在计算特征点上。
-
使用特征点时,忽略了除特征点以外的所有信息。一张图像有几十万个像素,而特征
点只有几百个。只使用特征点丢弃了大部分可能有用的图像信息。
-
相机有时会运动到特征缺失的地方,往往这些地方没有明显的纹理信息。例如,有时
我们会面对一堵白墙,或者一个空荡荡的走廓。这些场景下特征点数量会明显减少,
我们可能找不到足够的匹配点来计算相机运动。
我们看到使用特征点确实存在一些问题。有没有什么办法能够克服这些缺点呢?我们
有以下几种思路:
- 保留特征点,但只计算关键点,不计算描述子。同时,使用光流法(Optical Flow)来
跟踪特征点的运动。这样可以回避计算和匹配描述子带来的时间,但光流本身的计算
需要一定时间;
- 只计算关键点,不计算描述子。同时,使用直接法(Direct Method)来计算特征点
在下一时刻图像的位置。这同样可以跳过描述子的计算过程,而且直接法的计算更加
简单。
- 既不计算关键点、也不计算描述子,而是根据像素灰度的差异,直接计算相机运动。
第一种方法仍然使用特征点,只是把匹配描述子替换成了光流跟踪,估计相机运动时
仍使用对极几何、PnP 或 ICP 算法。而在后两个方法中,我们会根据图像的像素灰度信
息来计算相机运动,它们都称为直接法。(在直接法中,我们并不需要知道点与点之间之间的对应关系,而是通过最小化光度误差(Photometric error)来求得它们。)
直接法是从光流演变而来的。它们非常相似,具有相同的假设条件。光流描述了像素
在图像中的运动,而直接法则附带着一个相机运动模型。
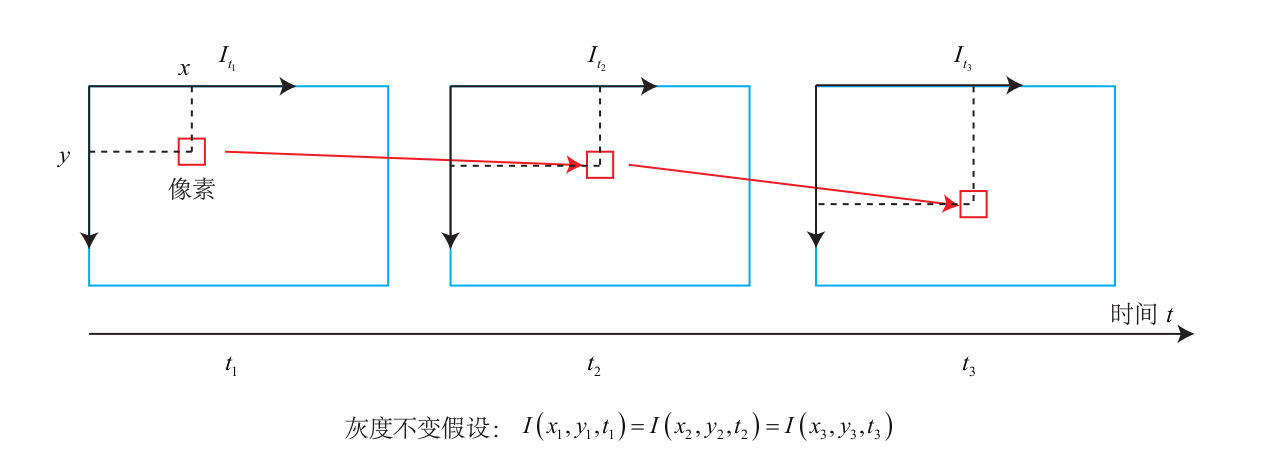
光流是一种描述像素随着时间,在图像之间运动的方法,如图 8-1 所示。随着时间的
经过,同一个像素会在图像中运动,而我们希望追踪它的运动过程。计算部分像素运动的
称为稀疏光流,计算所有像素的称为稠密光流。稀疏光流以 Lucas-Kanade 光流为代表,并
可以在 SLAM 中用于跟踪特征点位置。
在 LK 光流中,我们认为来自相机的图像是随时间变化的。图像可以看作时间的函数:
$\boldsymbol{I}(t)$。那么,一个在 t 时刻,位于 (x, y) 处的像素,它的灰度可以写成
$$
\boldsymbol{I}(x,y,t)
$$
这种方式把图像看成了关于位置与时间的函数,它的值域就是图像中像素的灰度。现在考
虑某个固定的空间点,它在 t 时刻的像素坐标为 x, y。由于相机的运动,它的图像坐标将
发生变化。我们希望估计这个空间点在其他时刻里图像的位置。怎么估计呢?这里要引入
光流法的基本假设:
灰度不变假设:同一个空间点的像素灰度值,在各个图像中是固定不变的。
对于 t 时刻位于 (x, y) 处的像素,我们设 t + dt 时刻,它运动到 (x + dx, y + dy) 处。
由于灰度不变,我们有:
$$
\boldsymbol{I}(x + dx, y + dy, t + dt) = \mathbf{I}(x,y,t)
$$
灰度不变假设是一个很强的假设,实际当中很可能不成立。事实上,由于物体的材质
不同,像素会出现高光和阴影部分;有时,相机会自动调整曝光参数,使得图像整体变亮
或变暗。这些时候灰度不变假设都是不成立的,因此光流的结果也不一定可靠。
对左边进行泰勒展开,保留一阶项,得:
$$
\boldsymbol{I}(x+\mathrm{d} x, y+\mathrm{d} y, t+\mathrm{d} t) \approx \boldsymbol{I}(x, y, t)+\frac{\partial \boldsymbol{I}}{\partial x} \mathrm{d} x+\frac{\partial \boldsymbol{I}}{\partial y} \mathrm{d} y+\frac{\partial \boldsymbol{I}}{\partial t} \mathrm{d} t
$$
因为我们假设了灰度不变,于是下一个时刻的灰度等于之前的灰度,从而
$$
\frac{\partial \boldsymbol{I}}{\partial x} \mathrm{d} x+\frac{\partial \boldsymbol{I}}{\partial y} \mathrm{d} y+\frac{\partial \boldsymbol{I}}{\partial t} \mathrm{d} t=0
$$
两边除以 dt,得:
$$
\frac{\partial \boldsymbol{I}}{\partial x} \frac{\mathrm{d} x}{\mathrm{d} t}+\frac{\partial \boldsymbol{I}}{\partial y} \frac{\mathrm{d} y}{\mathrm{d} t}=-\frac{\partial \boldsymbol{I}}{\partial t}
$$
其中 dx/dt 为像素在 x 轴上运动速度,而 dy/dt 为 y 轴速度,把它们记为 u, v。同
时 $\frac{\partial \boldsymbol{I}}{\partial x}$为图像在该点处 x 方向的梯度,另一项则是在 y 方向的梯度,记为 $\boldsymbol{I} _x, \boldsymbol{I}_y$ 。把图像灰度对时间的变化量记为 $\boldsymbol{I}_t$ ,写成矩阵形式,有:
$$
\left[\begin{array}{ll}{\boldsymbol{I}_{x}} & {\boldsymbol{I}_{y}}\end{array}\right]\left[\begin{array}{l}{u} \\ {v}\end{array}\right]=-\boldsymbol{I}_{t}
$$
我们想计算的是像素的运动 u, v,但是该式是带有两个变量的一次方程,仅凭它无法
计算出 u, v。因此,必须引入额外的约束来计算 u, v。在 LK 光流中,我们假设某一个窗
口内的像素具有相同的运动。
考虑一个大小为 w × w 大小的窗口,它含有 $w^2$数量的像素。由于该窗口内像素具有
同样的运动,因此我们共有 $w^2$ 个方程:
$$
\left[\begin{array}{ll}{\boldsymbol{I}_{x}} & {\boldsymbol{I}_{y}}\end{array}\right]_{k}\left[\begin{array}{l}{u} \\ {v}\end{array}\right]=-\boldsymbol{I}_{t k}, \quad k=1, \ldots, w^{2}
$$
记:
$$
\boldsymbol{A}=\left[\begin{array}{c}{\left[\boldsymbol{I}_{x}, \boldsymbol{I}_{y}\right]_{1}} \\ {\vdots} \\ {\left[\boldsymbol{I}_{x}, \boldsymbol{I}_{y}\right]_{k}}\end{array}\right], \boldsymbol{b}=\left[\begin{array}{c}{\boldsymbol{I}_{t 1}} \\ {\vdots} \\ {\boldsymbol{I}_{t k}}\end{array}\right]
$$
于是整个方程:
$$
A\left[\begin{array}{l}{u} \ {v}\end{array}\right]=-b
$$
这是一个关于 u, v 的超定线性方程,传统解法是求最小二乘解。
$$
\left[\begin{array}{l}{u} \ {v}\end{array}\right]^{*}=-\left(\boldsymbol{A}^{T} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{T} \boldsymbol{b}
$$
这样就得到了像素在图像间的运动速度 u, v。当 t 取离散的时刻而不是连续时间时,我
们可以估计某块像素在若干个图像中出现的位置。由于像素梯度仅在局部有效,所以如果
一次迭代不够好的话,我们会多迭代几次这个方程。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
|
#include <iostream>
#include <fstream>
#include <list>
#include <vector>
#include <chrono>
using namespace std;
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/features2d/features2d.hpp>
#include <opencv2/video/tracking.hpp>
int main( int argc, char** argv )
{
if ( argc != 2 )
{
cout<<"usage: useLK path_to_dataset"<<endl;
return 1;
}
string path_to_dataset = argv[1];
string associate_file = path_to_dataset + "/associate.txt";
ifstream fin( associate_file );
if ( !fin )
{
cerr<<"I cann't find associate.txt!"<<endl;
return 1;
}
string rgb_file, depth_file, time_rgb, time_depth;
list< cv::Point2f > keypoints; // 因为要删除跟踪失败的点,使用list
cv::Mat color, depth, last_color;
for ( int index=0; index<100; index++ )
{
fin>>time_rgb>>rgb_file>>time_depth>>depth_file;
color = cv::imread( path_to_dataset+"/"+rgb_file );
depth = cv::imread( path_to_dataset+"/"+depth_file, -1 );
if (index ==0 )
{
// 对第一帧提取FAST特征点
vector<cv::KeyPoint> kps;
cv::Ptr<cv::FastFeatureDetector> detector = cv::FastFeatureDetector::create();
detector->detect( color, kps );
for ( auto kp:kps )
keypoints.push_back( kp.pt );
last_color = color;
continue;
}
if ( color.data==nullptr || depth.data==nullptr )
continue;
// 对其他帧用LK跟踪特征点
vector<cv::Point2f> next_keypoints;
vector<cv::Point2f> prev_keypoints;
for ( auto kp:keypoints )
prev_keypoints.push_back(kp);
vector<unsigned char> status;
vector<float> error;
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
cv::calcOpticalFlowPyrLK( last_color, color, prev_keypoints, next_keypoints, status, error );
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>( t2-t1 );
cout<<"LK Flow use time:"<<time_used.count()<<" seconds."<<endl;
// 把跟丢的点删掉,因为要删除跟踪失败的点,使用list,而不是vector
// keypoint 的数目会逐渐减少
int i=0;
for ( auto iter=keypoints.begin(); iter!=keypoints.end(); i++)
{
if ( status[i] == 0 )
{
iter = keypoints.erase(iter);
continue;
}
*iter = next_keypoints[i];
iter++;
}
cout<<"tracked keypoints: "<<keypoints.size()<<endl;
if (keypoints.size() == 0)
{
cout<<"all keypoints are lost."<<endl;
break;
}
// 画出 keypoints
cv::Mat img_show = color.clone();
for ( auto kp:keypoints )
cv::circle(img_show, kp, 10, cv::Scalar(0, 240, 0), 1);
cv::imshow("corners", img_show);
cv::waitKey(0);
last_color = color;
}
return 0;
}
|
LK 光流跟踪能够直接得到特征点的对应关系。这个对应关系就像是描述子的匹配,但实际上我们大多数时候只会碰到特征点跟丢的情况,而不太会遇到误匹配,这应该是光流相对于描述子的一点优势。但是,匹配描述子的方法在相机运动较大时仍能成功,而光流必须要求相机运动是微小的。从这方面来说,光流的鲁棒性比描述子差一些。
考虑某个空间点$ P$ 和两个时刻的相机。$P$ 的世界坐标为 [X, Y, Z],它
在两个相机上成像,记非齐次像素坐标为$ p_ 1 , p_ 2 $。我们的目标是求第一个相机到第二个相
机的相对位姿变换。我们以第一个相机为参照系,设第二个相机旋转和平移为 $R, t$,对应李代数为$\xi$
$$
\begin{array}{l}{p_{1}=\left[\begin{array}{c}{u} \\ {v} \\ {1}\end{array}\right]_{1}=\frac{1}{Z_{1}} K P} \\ {p_{2}=\left[\begin{array}{c}{u} \\ {v} \\ {1}\end{array}\right]=\frac{1}{Z_{2}} K(R P+t)=\frac{1}{Z_{2}} K\left(\exp \left(\xi^{\wedge}\right) P\right)_{1 : 3}}\end{array}
$$
在直接法中,由于没有特征匹配,我们无从知道哪一个 $p _2$ 与 $p_1$ 对应
着同一个点。直接法的思路是根据当前相机的位姿估计值,来寻找$ p_ 2$ 的位置。但若相机
位姿不够好,$p_ 2 $的外观和$ p_ 1$ 会有明显差别。于是,为了减小这个差别,我们优化相机的
位姿,来寻找与 $p_ 1$ 更相似的$ p_ 2$ 。这同样可以通过解一个优化问题,但此时最小化的不是
重投影误差,而是光度误差(Photometric Error),也就是 $P$ 的两个像的亮度误差:
$$
e=\boldsymbol{I}_{1}\left(\boldsymbol{p}_{1}\right)-\boldsymbol{I}_{2}\left(\boldsymbol{p}_{2}\right)
$$
在直接法中,我们假设一个空间点
在各个视角下,成像的灰度是不变的。能够做这种优化的理由,仍是基于灰度不变假设。我们有许多个(比如 N 个)空间点 P i ,那么,整
个相机位姿估计问题变为:
$$
\min _{\xi} J(\boldsymbol{\xi})=\sum_{i=1}^{N} e_{i}^{T} e_{i}, \quad e_{i}=\boldsymbol{I}_{1}\left(\boldsymbol{p}_{1, i}\right)-\boldsymbol{I}_{2}\left(\boldsymbol{p}_{2, i}\right)
$$
注意这里的优化变量是相机位姿 $\boldsymbol{\xi}$。为了求解这个优化问题,我们关心误差 e 是如何
随着相机位姿 $\boldsymbol{\xi}$变化的,需要分析它们的导数关系。因此,使用李代数上的扰动模型。我
们给 $exp(\xi)$ 左乘一个小扰动$ exp(\delta \xi)$,得:
$$
\begin{aligned} e(\boldsymbol{\xi} \oplus \delta \boldsymbol{\xi}) &=\boldsymbol{I}_{1}\left(\frac{1}{Z_{1}} \boldsymbol{K} \boldsymbol{P}\right)-\boldsymbol{I}_{2}\left(\frac{1}{Z_{2}} \boldsymbol{K} \exp \left(\delta \boldsymbol{\xi}^{\wedge}\right) \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{P}\right) \\ & \approx \boldsymbol{I}_{1}\left(\frac{1}{Z_{1}} \boldsymbol{K} \boldsymbol{P}\right)-\boldsymbol{I}_{2}\left(\frac{1}{Z_{2}} \boldsymbol{K}\left(1+\delta \boldsymbol{\xi}^{\wedge}\right) \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{P}\right) \\ &=\boldsymbol{I}_{1}\left(\frac{1}{Z_{1}} \boldsymbol{K} \boldsymbol{P}\right)-\boldsymbol{I}_{2}\left(\frac{1}{Z_{2}} \boldsymbol{K} \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{P}+\frac{1}{Z_{2}} \boldsymbol{K} \delta \boldsymbol{\xi}^{\wedge} \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{P}\right) \end{aligned}
$$
记:
$$
\begin{aligned} \boldsymbol{q} &=\delta \boldsymbol{\xi}^{\wedge} \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{P} \ \boldsymbol{u} &=\frac{1}{Z_{2}} \boldsymbol{K} \boldsymbol{q} \end{aligned}
$$
这里的 $\boldsymbol{q}$ 为$\boldsymbol{ P}$ 在扰动之后,位于第二个相机坐标系下的坐标,而 $u$ 为它的像素坐标。
利用一阶泰勒展开,有:
$$
\begin{aligned} e(\boldsymbol{\xi} \oplus \delta \boldsymbol{\xi}) &=\boldsymbol{I}_{1}\left(\frac{1}{Z_{1}} \boldsymbol{K} \boldsymbol{P}\right)-\boldsymbol{I}_{2}\left(\frac{1}{Z_{2}} \boldsymbol{K} \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{P}+\boldsymbol{u}\right) \\ & \approx \boldsymbol{I}_{1}\left(\frac{1}{Z_{1}} \boldsymbol{K} \boldsymbol{P}\right)-\boldsymbol{I}_{2}\left(\frac{1}{Z_{2}} \boldsymbol{K} \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{P}\right)-\frac{\partial \boldsymbol{I}_{2}}{\partial \boldsymbol{u}} \frac{\partial \boldsymbol{u}}{\partial \boldsymbol{q}} \frac{\partial \boldsymbol{q}}{\partial \boldsymbol{g}} \frac{\partial \boldsymbol{q}}{\partial \delta \xi} \delta \boldsymbol{\xi} \\ &=e(\boldsymbol{\xi})-\frac{\partial \boldsymbol{I}_{2}}{\partial \boldsymbol{u}} \frac{\partial \boldsymbol{u}}{\partial \boldsymbol{q}} \frac{\partial \boldsymbol{q}}{\partial \delta \xi} \delta \boldsymbol{\xi} \end{aligned}
$$
我们看到,一阶导数由于链式法则分成了三项,而这三项都是容易计算的:
1 . $\frac{\partial \boldsymbol{I}_{2}}{\partial \boldsymbol{u}}$ 为 $u$ 处的像素梯度;
2 . $\frac{\partial \boldsymbol{u}}{\partial \boldsymbol{q}}$ 为投影方程关于相机坐标系下的三维点的导数。记 $q = [X, Y, Z] ^T$ ,根据上一
节的推导,导数为:
$$
\frac{\partial \boldsymbol{u}}{\partial \boldsymbol{q}}=\left[\begin{array}{ccc}{\frac{\partial u}{\partial X}} & {\frac{\partial u}{\partial Y}} & {\frac{\partial u}{\partial Z}} \\ {\frac{\partial v}{\partial X}} & {\frac{\partial v}{\partial Y}} & {\frac{\partial v}{\partial Z}}\end{array}\right]=\left[\begin{array}{ccc}{\frac{f_{x}}{Z}} & {0} & {-\frac{f_{x} X}{Z^{2}}} \\ {0} & {\frac{f_{y}}{Z}} & {-\frac{f_{y} Y}{Z^{2}}}\end{array}\right]
$$
3 . $\frac{\partial \boldsymbol{q}}{\partial \delta \xi}$ 为变换后的三维点对变换的导数:
$$
\frac{\partial \boldsymbol{q}}{\partial \delta \boldsymbol{\xi}}=\left[\boldsymbol{I},-\boldsymbol{q}^{\wedge}\right]
$$
由于后两项只与三维点 q 有关,而与图像无关,我们经常把它合并在一起:
$$
\frac{\partial u}{\partial \delta \xi}=\left[\begin{array}{cccccc}{\frac{f_{x}}{Z}} & {0} & {-\frac{f_{x} X}{Z^{2}}} & {-\frac{f_{x} X Y}{Z^{2}}} & {f_{x}+\frac{f_{x} X^{2}}{Z^{2}}} & {-\frac{f_{x} Y}{Z}} \\ {0} & {\frac{f_{y}}{Z}} & {-\frac{f_{y} Y}{Z^{2}}} & {-f_{y}-\frac{f_{y} Y^{2}}{Z^{2}}} & {\frac{f_{y} X Y}{Z^{2}}} & {\frac{f_{y} X}{Z}}\end{array}\right]
$$
于是,我们推导了误差相对于李代数的雅可
比矩阵:
$$
\boldsymbol{J}=-\frac{\partial \boldsymbol{I}_{2}}{\partial \boldsymbol{u}} \frac{\partial \boldsymbol{u}}{\partial \boldsymbol{\xi}}
$$
对于 N 个点的问题,我们可以用这种方法计算优化问题的雅可比,然后使用 G-N 或
L-M 计算增量,迭代求解。
P 是一个已知位置的空间点,根据 P 的来源,我们可以把直接法进行分类:
-
P 来自于稀疏关键点,我们称之为稀疏直接法。通常我们使用数百个至上千个关键
点,并且像 L-K 光流那样,假设它周围像素也是不变的。这种稀疏直接法不必计算
描述子,并且只使用数百个像素,因此速度最快,但只能计算稀疏的重构。
-
P 来自部分像素。我们看到式(8.16)中,如果像素梯度为零,整一项雅可比就为零,
不会对计算运动增量有任何贡献。因此,可以考虑只使用带有梯度的像素点,舍弃像
素梯度不明显的地方。这称之为半稠密(Semi-Dense)的直接法,可以重构一个半稠
密结构。
-
P 为所有像素,称为稠密直接法。稠密重构需要计算所有像素(一般几十万至几百万
个),因此多数不能在现有的 CPU 上实时计算,需要 GPU 的加速。但是,如前面
所讨论的,梯度不明显的点,在运动估计中不会有太大贡献,在重构时也会难以估计
位置。
在使用 g2o之前,需要把直接法抽象成一个图优化问题。显然,直接法是由以下顶点和边组成的:
-
优化变量为一个相机位姿,因此需要一个位姿顶点。由于我们在推导中使用了李代
数,故程序中使用李代数表达的 SE(3) 位姿顶点。与上一章一样,我们将使用“Ver-
texSE3Expmap”作为相机位姿。
-
误差项为单个像素的光度误差。由于整个优化过程中 I 1 (p 1 ) 保持不变,我们可以把
它当成一个固定的预设值,然后调整相机位姿,使 I 2 (p 2 ) 接近这个值。于是,这种
边只连接一个顶点,为一元边。由于 g2o 中本身没有计算光度误差的边,我们需要
自己定义一种新的边。
在上述的建模中,直接法图优化问题是由一个相机位姿顶点与许多条一元边组成的。
如果使用稀疏的直接法,那我们大约会有几百至几千条这样的边;稠密直接法则会有几十
万条边。优化问题对应的线性方程是计算李代数增量,本身规模不大(6×6)
,所以主要的
计算时间会花费在每条边的误差与雅可比的计算上。下面的实验中,我们先来定义一种用
于直接法位姿估计的边,然后,使用该边构建图优化问题并求解之。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
|
#include <iostream>
#include <fstream>
#include <list>
#include <vector>
#include <chrono>
#include <ctime>
#include <climits>
#include <opencv2/core/core.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/features2d/features2d.hpp>
#include <g2o/core/base_unary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/solvers/dense/linear_solver_dense.h>
#include <g2o/core/robust_kernel.h>
#include <g2o/types/sba/types_six_dof_expmap.h>
using namespace std;
using namespace g2o;
/********************************************
* 本节演示了RGBD上的稀疏直接法
********************************************/
// 一次测量的值,包括一个世界坐标系下三维点与一个灰度值
struct Measurement
{
Measurement ( Eigen::Vector3d p, float g ) : pos_world ( p ), grayscale ( g ) {}
Eigen::Vector3d pos_world;
float grayscale;
};
inline Eigen::Vector3d project2Dto3D ( int x, int y, int d, float fx, float fy, float cx, float cy, float scale )
{
float zz = float ( d ) /scale;
float xx = zz* ( x-cx ) /fx;
float yy = zz* ( y-cy ) /fy;
return Eigen::Vector3d ( xx, yy, zz );
}
inline Eigen::Vector2d project3Dto2D ( float x, float y, float z, float fx, float fy, float cx, float cy )
{
float u = fx*x/z+cx;
float v = fy*y/z+cy;
return Eigen::Vector2d ( u,v );
}
// 直接法估计位姿
// 输入:测量值(空间点的灰度),新的灰度图,相机内参; 输出:相机位姿
// 返回:true为成功,false失败
bool poseEstimationDirect ( const vector<Measurement>& measurements, cv::Mat* gray, Eigen::Matrix3f& intrinsics, Eigen::Isometry3d& Tcw );
// project a 3d point into an image plane, the error is photometric error
// an unary edge with one vertex SE3Expmap (the pose of camera)
class EdgeSE3ProjectDirect: public BaseUnaryEdge< 1, double, VertexSE3Expmap>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
EdgeSE3ProjectDirect() {}
EdgeSE3ProjectDirect ( Eigen::Vector3d point, float fx, float fy, float cx, float cy, cv::Mat* image )
: x_world_ ( point ), fx_ ( fx ), fy_ ( fy ), cx_ ( cx ), cy_ ( cy ), image_ ( image )
{}
//虚函数重写 误差项
virtual void computeError()
{
const VertexSE3Expmap* v =static_cast<const VertexSE3Expmap*> ( _vertices[0] );
Eigen::Vector3d x_local = v->estimate().map ( x_world_ );
float x = x_local[0]*fx_/x_local[2] + cx_;
float y = x_local[1]*fy_/x_local[2] + cy_;
// check x,y is in the image
if ( x-4<0 || ( x+4 ) >image_->cols || ( y-4 ) <0 || ( y+4 ) >image_->rows )
{
_error ( 0,0 ) = 0.0;
this->setLevel ( 1 );
}
else
{
_error ( 0,0 ) = getPixelValue ( x,y ) - _measurement;
}
}
// plus in manifold
virtual void linearizeOplus( )
{
if ( level() == 1 )
{
_jacobianOplusXi = Eigen::Matrix<double, 1, 6>::Zero();
return;
}
VertexSE3Expmap* vtx = static_cast<VertexSE3Expmap*> ( _vertices[0] );
Eigen::Vector3d xyz_trans = vtx->estimate().map ( x_world_ ); // q in book
double x = xyz_trans[0];
double y = xyz_trans[1];
double invz = 1.0/xyz_trans[2];
double invz_2 = invz*invz;
float u = x*fx_*invz + cx_;
float v = y*fy_*invz + cy_;
// jacobian from se3 to u,v
// NOTE that in g2o the Lie algebra is (\omega, \epsilon), where \omega is so(3) and \epsilon the translation
Eigen::Matrix<double, 2, 6> jacobian_uv_ksai;
jacobian_uv_ksai ( 0,0 ) = - x*y*invz_2 *fx_;
jacobian_uv_ksai ( 0,1 ) = ( 1+ ( x*x*invz_2 ) ) *fx_;
jacobian_uv_ksai ( 0,2 ) = - y*invz *fx_;
jacobian_uv_ksai ( 0,3 ) = invz *fx_;
jacobian_uv_ksai ( 0,4 ) = 0;
jacobian_uv_ksai ( 0,5 ) = -x*invz_2 *fx_;
jacobian_uv_ksai ( 1,0 ) = - ( 1+y*y*invz_2 ) *fy_;
jacobian_uv_ksai ( 1,1 ) = x*y*invz_2 *fy_;
jacobian_uv_ksai ( 1,2 ) = x*invz *fy_;
jacobian_uv_ksai ( 1,3 ) = 0;
jacobian_uv_ksai ( 1,4 ) = invz *fy_;
jacobian_uv_ksai ( 1,5 ) = -y*invz_2 *fy_;
Eigen::Matrix<double, 1, 2> jacobian_pixel_uv;
jacobian_pixel_uv ( 0,0 ) = ( getPixelValue ( u+1,v )-getPixelValue ( u-1,v ) ) /2;
jacobian_pixel_uv ( 0,1 ) = ( getPixelValue ( u,v+1 )-getPixelValue ( u,v-1 ) ) /2;
//雅克比矩阵
_jacobianOplusXi = jacobian_pixel_uv*jacobian_uv_ksai;
}
// dummy read and write functions because we don't care...
virtual bool read ( std::istream& in ) {}
virtual bool write ( std::ostream& out ) const {}
protected:
// get a gray scale value from reference image (bilinear interpolated)
inline float getPixelValue ( float x, float y )
{
uchar* data = & image_->data[ int ( y ) * image_->step + int ( x ) ];
float xx = x - floor ( x );
float yy = y - floor ( y );
return float (
( 1-xx ) * ( 1-yy ) * data[0] +
xx* ( 1-yy ) * data[1] +
( 1-xx ) *yy*data[ image_->step ] +
xx*yy*data[image_->step+1]
);
}
public:
Eigen::Vector3d x_world_; // 3D point in world frame
float cx_=0, cy_=0, fx_=0, fy_=0; // Camera intrinsics
cv::Mat* image_=nullptr; // reference image
};
int main ( int argc, char** argv )
{
if ( argc != 2 )
{
cout<<"usage: useLK path_to_dataset"<<endl;
return 1;
}
srand ( ( unsigned int ) time ( 0 ) );
string path_to_dataset = argv[1];
string associate_file = path_to_dataset + "/associate.txt";
ifstream fin ( associate_file );
string rgb_file, depth_file, time_rgb, time_depth;
cv::Mat color, depth, gray;
vector<Measurement> measurements;
// 相机内参
float cx = 325.5;
float cy = 253.5;
float fx = 518.0;
float fy = 519.0;
float depth_scale = 1000.0;
Eigen::Matrix3f K;
K<<fx,0.f,cx,0.f,fy,cy,0.f,0.f,1.0f;
Eigen::Isometry3d Tcw = Eigen::Isometry3d::Identity();
cv::Mat prev_color;
// 我们以第一个图像为参考,对后续图像和参考图像做直接法
for ( int index=0; index<10; index++ )
{
cout<<"*********** loop "<<index<<" ************"<<endl;
fin>>time_rgb>>rgb_file>>time_depth>>depth_file;
color = cv::imread ( path_to_dataset+"/"+rgb_file );
depth = cv::imread ( path_to_dataset+"/"+depth_file, -1 );
if ( color.data==nullptr || depth.data==nullptr )
continue;
cv::cvtColor ( color, gray, cv::COLOR_BGR2GRAY );
if ( index ==0 )
{
// 对第一帧提取FAST特征点
vector<cv::KeyPoint> keypoints;
cv::Ptr<cv::FastFeatureDetector> detector = cv::FastFeatureDetector::create();
detector->detect ( color, keypoints );
for ( auto kp:keypoints )
{
// 去掉邻近边缘处的点
if ( kp.pt.x < 20 || kp.pt.y < 20 || ( kp.pt.x+20 ) >color.cols || ( kp.pt.y+20 ) >color.rows )
continue;
ushort d = depth.ptr<ushort> ( cvRound ( kp.pt.y ) ) [ cvRound ( kp.pt.x ) ];
if ( d==0 )
continue;
//获取第一帧特征点的世界坐标做参考坐标,后面帧的R,t都是相对于第一帧来讲
Eigen::Vector3d p3d = project2Dto3D ( kp.pt.x, kp.pt.y, d, fx, fy, cx, cy, depth_scale );
float grayscale = float ( gray.ptr<uchar> ( cvRound ( kp.pt.y ) ) [ cvRound ( kp.pt.x ) ] );
measurements.push_back ( Measurement ( p3d, grayscale ) );
}
prev_color = color.clone();
continue;
}
// 使用直接法计算相机运动
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
poseEstimationDirect ( measurements, &gray, K, Tcw );
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>> ( t2-t1 );
cout<<"direct method costs time: "<<time_used.count() <<" seconds."<<endl;
cout<<"Tcw="<<Tcw.matrix() <<endl;
// plot the feature points
cv::Mat img_show ( color.rows*2, color.cols, CV_8UC3 );
prev_color.copyTo ( img_show ( cv::Rect ( 0,0,color.cols, color.rows ) ) );
color.copyTo ( img_show ( cv::Rect ( 0,color.rows,color.cols, color.rows ) ) );
for ( Measurement m:measurements )
{
if ( rand() > RAND_MAX/5 )
continue;
Eigen::Vector3d p = m.pos_world;
Eigen::Vector2d pixel_prev = project3Dto2D ( p ( 0,0 ), p ( 1,0 ), p ( 2,0 ), fx, fy, cx, cy );
Eigen::Vector3d p2 = Tcw*m.pos_world;
Eigen::Vector2d pixel_now = project3Dto2D ( p2 ( 0,0 ), p2 ( 1,0 ), p2 ( 2,0 ), fx, fy, cx, cy );
if ( pixel_now(0,0)<0 || pixel_now(0,0)>=color.cols || pixel_now(1,0)<0 || pixel_now(1,0)>=color.rows )
continue;
float b = 255*float ( rand() ) /RAND_MAX;
float g = 255*float ( rand() ) /RAND_MAX;
float r = 255*float ( rand() ) /RAND_MAX;
cv::circle ( img_show, cv::Point2d ( pixel_prev ( 0,0 ), pixel_prev ( 1,0 ) ), 8, cv::Scalar ( b,g,r ), 2 );
cv::circle ( img_show, cv::Point2d ( pixel_now ( 0,0 ), pixel_now ( 1,0 ) +color.rows ), 8, cv::Scalar ( b,g,r ), 2 );
cv::line ( img_show, cv::Point2d ( pixel_prev ( 0,0 ), pixel_prev ( 1,0 ) ), cv::Point2d ( pixel_now ( 0,0 ), pixel_now ( 1,0 ) +color.rows ), cv::Scalar ( b,g,r ), 1 );
}
cv::imshow ( "result", img_show );
cv::waitKey ( 0 );
}
return 0;
}
bool poseEstimationDirect ( const vector< Measurement >& measurements, cv::Mat* gray, Eigen::Matrix3f& K, Eigen::Isometry3d& Tcw )
{
// 初始化g2o
typedef g2o::BlockSolver<g2o::BlockSolverTraits<6,1>> DirectBlock; // 求解的向量是6*1的
DirectBlock::LinearSolverType* linearSolver = new g2o::LinearSolverDense< DirectBlock::PoseMatrixType > ();
DirectBlock* solver_ptr = new DirectBlock ( linearSolver );
// g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr ); // G-N
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( solver_ptr ); // L-M
g2o::SparseOptimizer optimizer;
optimizer.setAlgorithm ( solver );
optimizer.setVerbose( true );
g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap();
pose->setEstimate ( g2o::SE3Quat ( Tcw.rotation(), Tcw.translation() ) );
pose->setId ( 0 );
optimizer.addVertex ( pose );
// 添加边
int id=1;
for ( Measurement m: measurements )
{
EdgeSE3ProjectDirect* edge = new EdgeSE3ProjectDirect (
m.pos_world,
K ( 0,0 ), K ( 1,1 ), K ( 0,2 ), K ( 1,2 ), gray
);
edge->setVertex ( 0, pose );
edge->setMeasurement ( m.grayscale );
edge->setInformation ( Eigen::Matrix<double,1,1>::Identity() );
edge->setId ( id++ );
optimizer.addEdge ( edge );
}
cout<<"edges in graph: "<<optimizer.edges().size() <<endl;
optimizer.initializeOptimization();
optimizer.optimize ( 30 );
Tcw = pose->estimate();
}
|
我们的边继承自 g2o::BaseUnaryEdge。在继承时,需要在模板参数里填入测量值的维
度、类型,以及连接此边的顶点,同时,我们把空间点 P 、相机内参和图像存储在该边的成
员变量中。为了让 g2o 优化该边对应的误差,我们需要覆写两个虚函数:用 computeError()
计算误差值,用 linearizeOplus() 计算雅可比。可以看到,这里的雅可比计算与式(8.16)
是一致的。注意我们在程序中的误差计算里,使用了 I 2 (p 2 ) − I 1 (p 1 ) 的形式,因此前面的
负号可以省去,只需把像素梯度乘以像素到李代数的梯度即可。
修改的部分:对参考帧中,先提取梯度较明显
的像素,然后用直接法,以这些像素为图优化边,来估计相机运动。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
// select the pixels with high gradiants
for ( int x=10; x<gray.cols-10; x++ )
for ( int y=10; y<gray.rows-10; y++ )
{
Eigen::Vector2d delta (
gray.ptr<uchar>(y)[x+1] - gray.ptr<uchar>(y)[x-1],
gray.ptr<uchar>(y+1)[x] - gray.ptr<uchar>(y-1)[x]
);
if ( delta.norm() < 50 )
continue;
ushort d = depth.ptr<ushort> (y)[x];
if ( d==0 )
continue;
Eigen::Vector3d p3d = project2Dto3D ( x, y, d, fx, fy, cx, cy, depth_scale );
float grayscale = float ( gray.ptr<uchar> (y) [x] );
measurements.push_back ( Measurement ( p3d, grayscale ) );
}
|
