
SFM(structure-from-motion)算法是一种基于各种收集到的无序图片进行三维重建的离线算法。顾名思义是从运动中(不同时间拍摄的图片集)恢复物体的三维结构,这需要估计出图片的$R,t$,结合相机内参重建稀疏点云。
SFM在多视图三维重建步骤中的对应位置
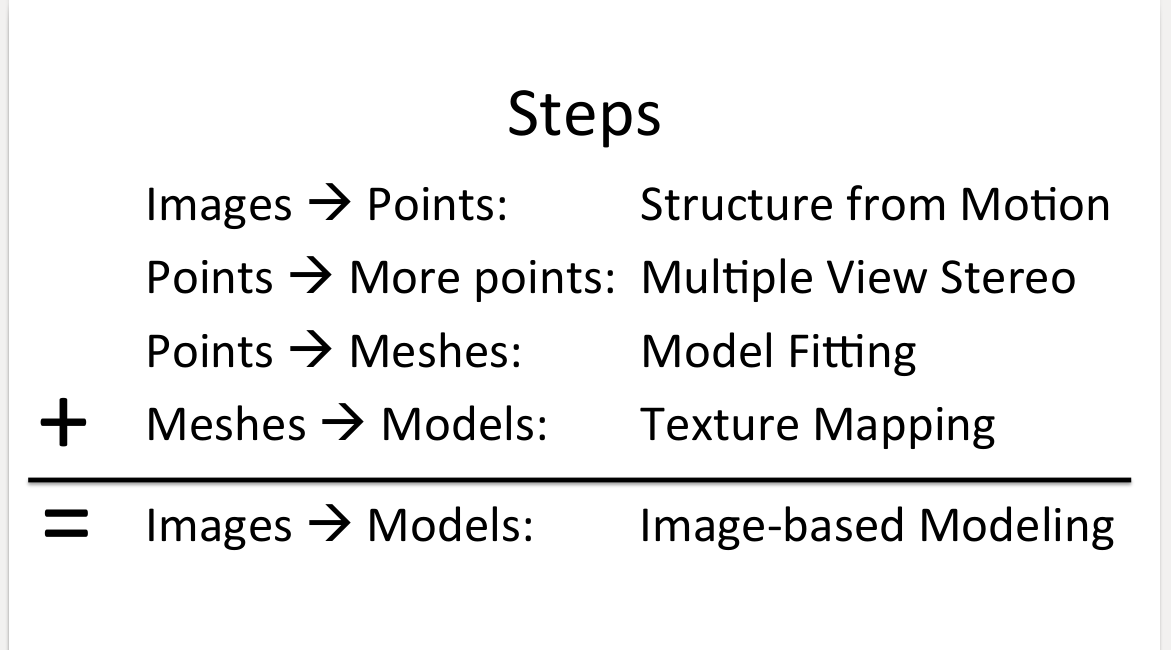 如上图,完整的多视图三维重建:重建稀疏点云–重建稠密点云–Mesh–纹理Texture。SFM负责重建稀疏点云这一部分。这需要从多张视图中估计出照片的旋转平移矩阵$R,t$,结合相机内参恢复物体稀疏点云结构。
如上图,完整的多视图三维重建:重建稀疏点云–重建稠密点云–Mesh–纹理Texture。SFM负责重建稀疏点云这一部分。这需要从多张视图中估计出照片的旋转平移矩阵$R,t$,结合相机内参恢复物体稀疏点云结构。
算法的关键是获得两张图片中的对应点,然后估计基础矩阵$F$,再估计本征矩阵$E$,再通过SVD分解求得较好的$R,t$,得到物体的三维点,最后将多个稀疏点云融合在一起,这里一个常用的算法是Bundle Adjustment(BA)。
算法原理
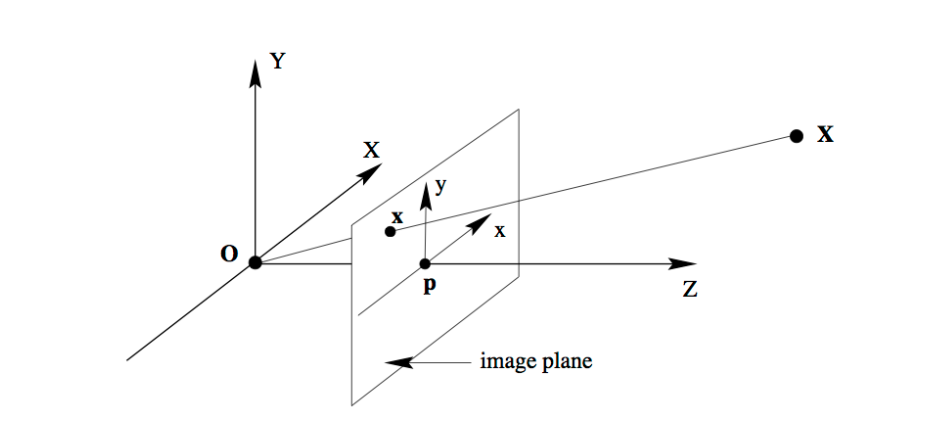 首先得了解物体在针孔相机模型下,由世界坐标系投影到像素坐标系的数学模型。图像中的像素坐标点$\mathbf{x}=\left[\begin{array}{l}{x} \\ {y}\end{array}\right]$和它在真实世界下的世界坐标点$\mathbf{X}=\left[\begin{array}{l}{X} \\ {Y} \\ {Z}\end{array}\right]$的对应关系为:
首先得了解物体在针孔相机模型下,由世界坐标系投影到像素坐标系的数学模型。图像中的像素坐标点$\mathbf{x}=\left[\begin{array}{l}{x} \\ {y}\end{array}\right]$和它在真实世界下的世界坐标点$\mathbf{X}=\left[\begin{array}{l}{X} \\ {Y} \\ {Z}\end{array}\right]$的对应关系为:
$$ \left[\begin{array}{l}{x} \\ {y} \\ {1}\end{array}\right]=\left[\begin{array}{lll}{f} & {0} & {0} \\ {0} & {f} & {0} \\ {0} & {0} & {1}\end{array}\right]\left[\begin{array}{cccc}{1} & {0} & {0} & {0} \\ {0} & {1} & {0} & {0} \\ {0} & {0} & {1} & {0}\end{array}\right]\left[\begin{array}{cc}{\mathbf{R}} & {\mathbf{t}} \\ {\mathbf{0}^{T}} & {1}\end{array}\right]\left[\begin{array}{c}{X} \\ {Y} \\ {Z} \\ {1}\end{array}\right] $$
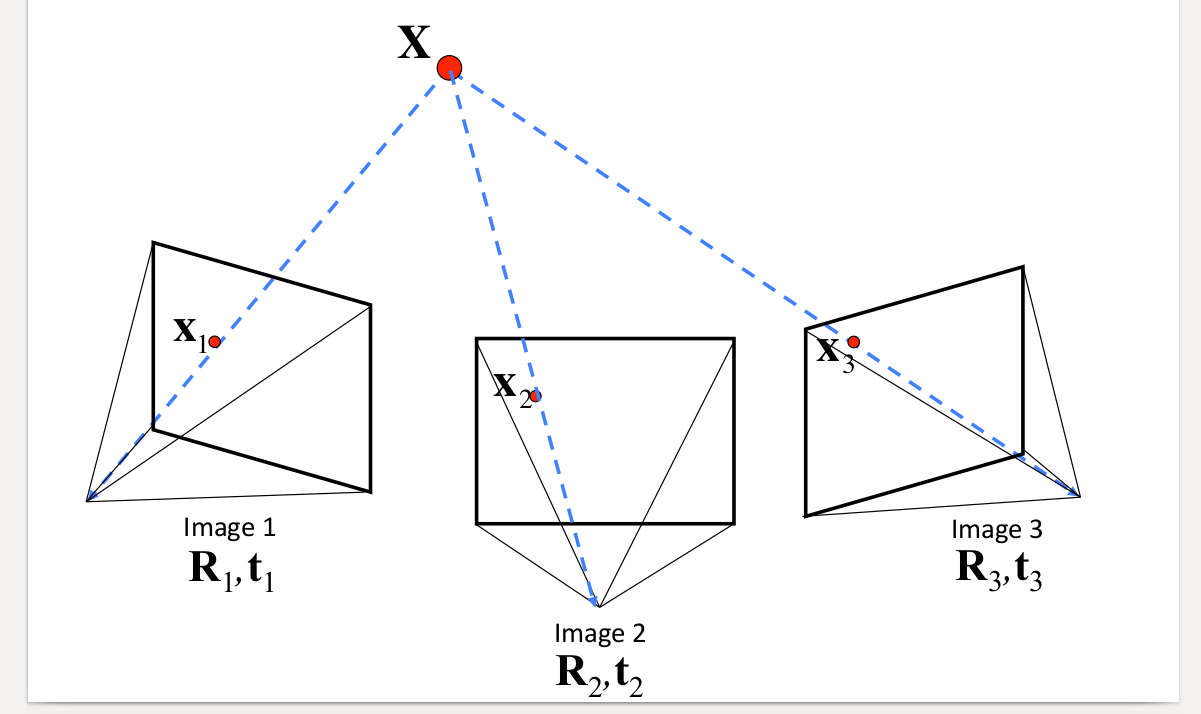
用矩阵形式表示: $$ \mathbf{x}=\mathbf{K}[\mathbf{R} | \mathbf{t}] \mathbf{X} $$ 或者: $$ \mathbf{x}=\mathbf{P} \mathbf{X} $$ 对于同一个世界坐标系下的点,在多个相机坐标系下成像,即为:
$$ \begin{aligned} \mathbf{x}_{1} &=\mathbf{K}\left[\mathbf{R}_{1} | \mathbf{t}_{1}\right] \mathbf{X} \\ \mathbf{x}_{2} &=\mathbf{K}\left[\mathbf{R}_{2} | \mathbf{t}_{2}\right] \mathbf{X} \\ \mathbf{x}_{3} &=\mathbf{K}\left[\mathbf{R}_{3} | \mathbf{t}_{3}\right] \mathbf{X} \end{aligned} $$
 如果能准确找到这些对应点,就可以准确计算出各相机的$R,t$,但事实上只能用估计的方法求得较好的对应点。一个思路是提取各图像中物体的特征点,常用的算法是SIFT,因其具有尺度和旋转不变性,再去做匹配,再用RANSC算法优化改善匹配对。之后利用F矩阵和E矩阵可以算出相机的$R,t$,再通过三角化得到稀疏点云,如下图:
如果能准确找到这些对应点,就可以准确计算出各相机的$R,t$,但事实上只能用估计的方法求得较好的对应点。一个思路是提取各图像中物体的特征点,常用的算法是SIFT,因其具有尺度和旋转不变性,再去做匹配,再用RANSC算法优化改善匹配对。之后利用F矩阵和E矩阵可以算出相机的$R,t$,再通过三角化得到稀疏点云,如下图:
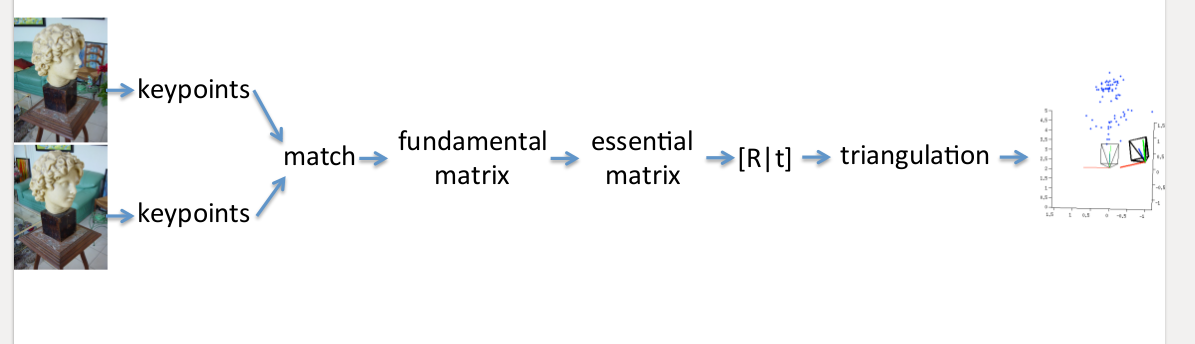
SIFT特征提取
参考这篇文章。
特征匹配
第二步是匹配和建立track,图像对两两匹配,一般采用欧式距离.有两种方法:
-
粗暴匹配,对所有特征点都穷举计算距离
-
邻近搜索,建立KD树,缩小搜索范围,能提高效率,但也有可能不是最优,所以邻域取值是关键,越大越准确,越大计算量越大
这里参考的是这篇文章。
然而初选的匹配对可能还是不可靠,需要用几何约束去检测。这个测试是基于事实的,假设一个静止场景,不是所有的匹配特征点在实际场景中是符合物理规律的。那么就需要计算对极几何,F矩阵可以把两张图片之间的像素坐标联系起来,并包含相机的内参信息。每一个符合的匹配对像素坐标都需要满足:
$$ \mathbf{x}_{1}^{T} \mathbf{F} \mathbf{x}_{2}=0 $$
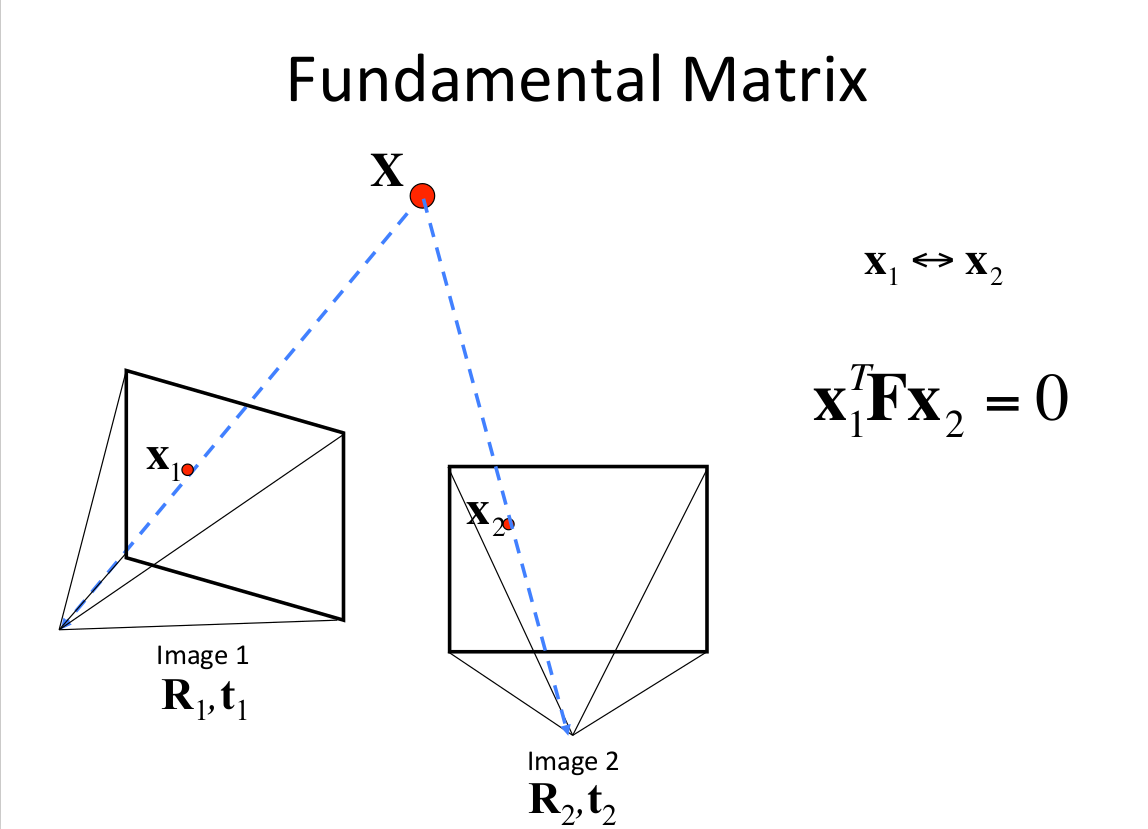 然而像这种F矩阵计算出有很多噪声数据,需要用RANSAC(随机抽样一致性)算法进行滤波,用直接线性变换(DLT)(需要八组对应点)来进行RANSACA假设,剔除不满足基础矩阵的匹配对。
然而像这种F矩阵计算出有很多噪声数据,需要用RANSAC(随机抽样一致性)算法进行滤波,用直接线性变换(DLT)(需要八组对应点)来进行RANSACA假设,剔除不满足基础矩阵的匹配对。

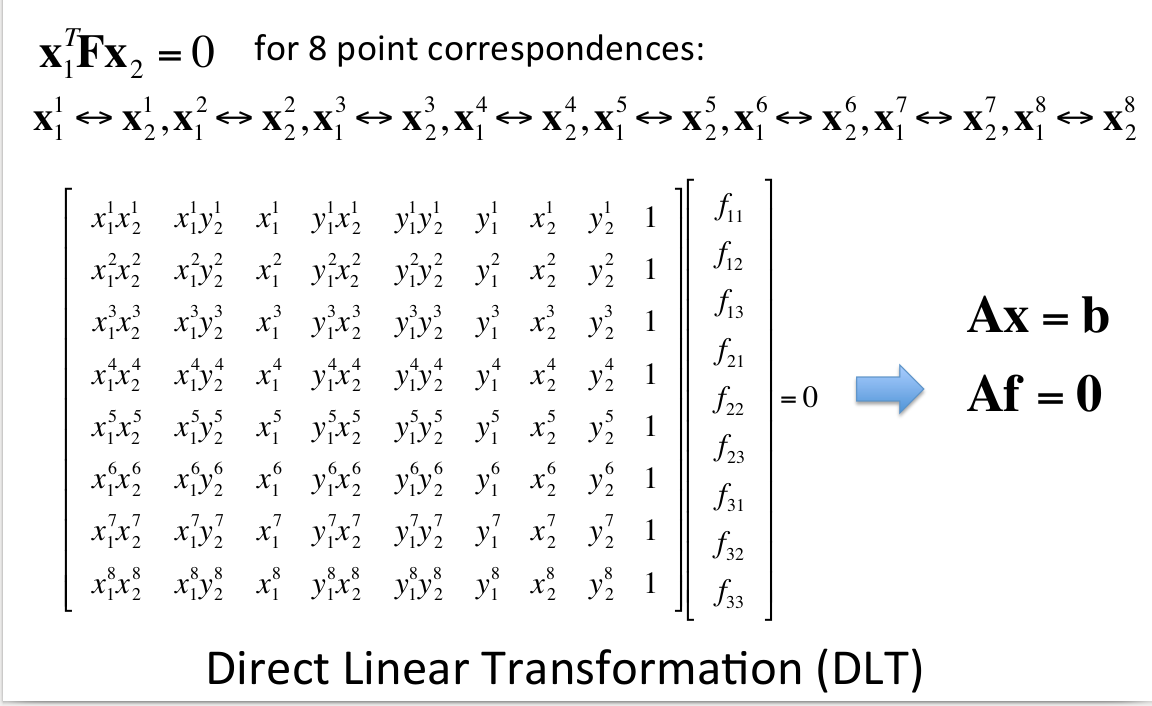
用RANSAC去估计基础矩阵F的思路是:
-
多次迭代以下流程:
-
选8个点
-
用DLT算法计算F
-
记录内点的数目
-
-
选取内点最多的对应F
这时候可以找到比较好的匹配点对了。
特征分解本征矩阵得到R,t
基础矩阵F和本征矩阵E的关系是:
$$ \begin{array}{l}{\mathbf{x}_{1}^{T} \mathbf{F} \mathbf{x}_{2}=0} \\ {\mathbf{E}=\mathbf{K}_{\mathbf{I}}^{T} \mathbf{F} \mathbf{K}_{2}}\end{array} $$
$R,t$可以由本征矩阵E经过SVD分解求得。
这里有一个问题,给定一个本征矩阵$\mathbf{E}=\mathbf{U} \operatorname{diag}(1,1,0) \mathbf{V}^{T}$ 和第一个相机矩阵 $\mathbf{P}_{1}=[\mathbf{I} | \mathbf{0}]$ ,第二个相机矩阵有以下几种选择:
$$ \begin{array}{l}{\mathbf{P}_{2}=\left[\mathbf{U} \mathbf{W} \mathbf{V}^{T} |+\mathbf{u}_{3}\right]} \\ {\mathbf{P}_{2}=\left[\mathbf{U} \mathbf{W} \mathbf{V}^{T} |-\mathbf{u}_{3}\right]} \\ {\mathbf{P}_{2}=\left[\mathbf{U} \mathbf{W}^{T} \mathbf{V}^{T} |+\mathbf{u}_{3}\right]} \\ {\mathbf{P}_{2}=\left[\mathbf{U} \mathbf{W}^{T} \mathbf{V}^{T} |-\mathbf{u}_{3}\right]}\end{array} \quad \mathbf{W}=\left[\begin{array}{ccc}{0} & {-1} & {0} \\ {1} & {0} & {0} \\ {0} & {0} & {1}\end{array}\right] $$
 我们希望得到上图中,图一的情况,这种情况下,两个相机的“从光心到主点的射线”与“三维物体点到光心的连线”的夹角都小于90度。
公式表示为:
我们希望得到上图中,图一的情况,这种情况下,两个相机的“从光心到主点的射线”与“三维物体点到光心的连线”的夹角都小于90度。
公式表示为:


选择$(\mathbf{X}-\mathbf{C}) \cdot \mathbf{R}(3, :)^{T}>0 ?$的对应的$P_2$即可。这时候两幅图像的$R,t$均求得。
点云融合
由上面计算出来的$R,t$和相机内参,可以恢复出物体的稀疏点云结构,如何将点云融合呢,如果求出的$R,t$是一个准确解,这时直接讲各部分点云通过$R,t$变换到同一基准下就可以完成融合的过程。单上面求解出来的$R,t$仍然不够准确,这时候可以通过Bundle Adjustment(BA),这是一个非线性优化的过程,目的是使重建误差降低到最小,通过调整POSE和三维点使反向投影差最小,如果相机没有标定,还应该将焦距也参与平差。BA最小化以下目标函数:
$$ \min \sum_{i} \sum_{j}\left(\tilde{\mathbf{x}}_{i}^{j}-\mathbf{K}\left[\mathbf{R}_{i} | \mathbf{t}_{i}\right] \mathbf{X}^{j}\right)^{2} $$
多幅图像的计算方法,依次迭代上面的流程,求得比较准确的$R,t$后,即可进行点云的融合,到此完成稀疏点云的重建过程。